前回の続きです。
前回は「要素 p が集合 Q に含まれるかどうか」を考えましたが、今回は「集合 P 全体が集合 Q にすっぽり含まれるか」を考えます(あるグループが別のグループの一部かどうか)
基本的な考え方は前回の場合と同じでいいと思います。
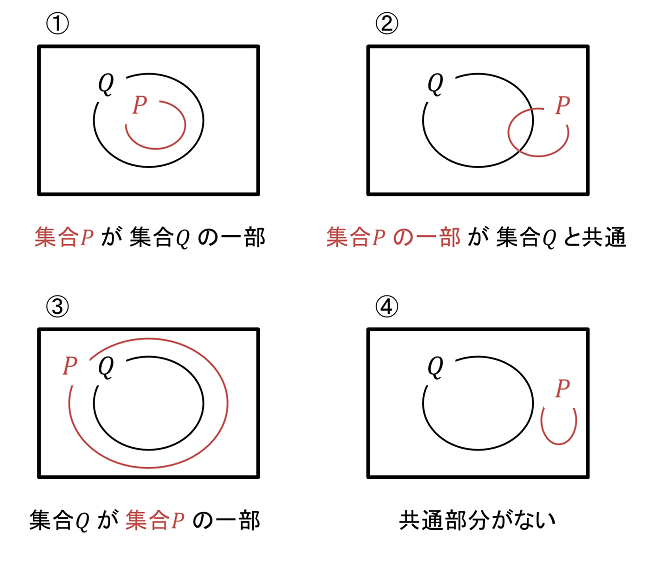
そもそも、集合 P と 集合 Q の関係性は以下の4パターンしかないわけです。
そのうち「p ⇒ q が真」というのは、① の場合に相当します(P が Q に含まれている)
| (図表1) 2つの集合の関係:そもそもこの4パターンのどれかでしかない ※ 厳密には P=Q の場合がありますが、それは ① に含めて扱います。
|
※ ②~④ は、一言で言うと「P の要素で、Q に属していないものがある」という状況です。
で、背理法における「命題の否定」というのは、この ① の否定(つまり ②~④ の場合)についてどうなるかを見ているのです。
そして、②~④ で何かしらおかしいことが生じれば、こうした状況は現実的には存在しえないということになります。
①~④ のうちの、②~④ が存在しえないということですので、消去法的に ①、つまり「P は Q の一部」というケースしか残らないということになります。
ということで、今回の場合も元の命題 p ⇒ q は「真」ということになるのです。
(図表2) 消去法的に ① しか残らない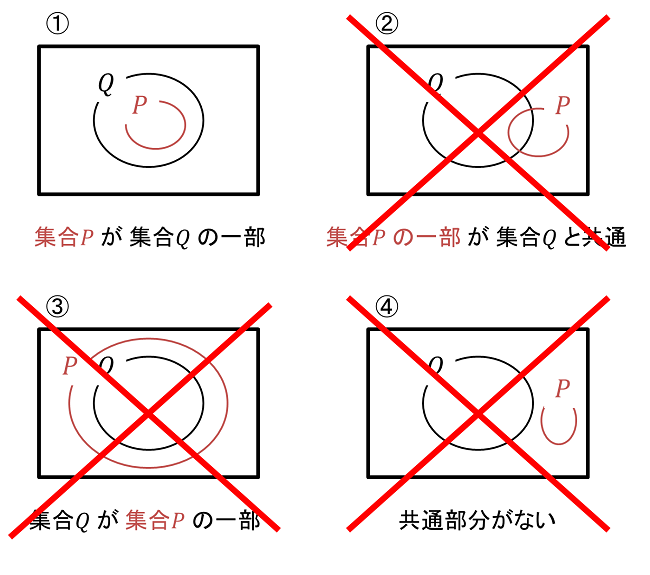 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |