そのため、箱ひげ図をつくるときには、「正しくデータを並べて読み取る」ということが重要になります。ひとつでもズレがあると、答えが変わってきてしまうためです。

 
 
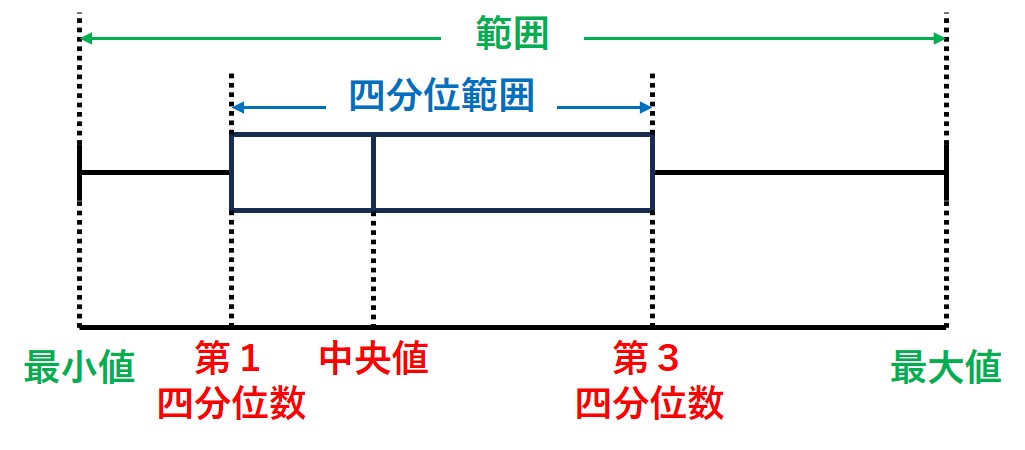
（２）箱ひげ図のつくり
まず、四分位範囲となる部分を「箱」で表しています。（第1四分位数～第3四分位数の範囲）
その箱は、中央値がとる値のところで区切られています。

その箱の両側から、「最小値と最大値に向かって」線が伸びているので、この線の両端がデータの範囲となります。
つまり、「箱ひげ図の両端を見れば、データの範囲が分かる」ということです。

＜補足＞

箱ひげ図で、長方形で表されている部分を「箱」、両側に伸びている線の部分を「ひげ」といいます。
そのため、「箱ひげ図」という名称になっています。

＜まとめ＞

・データの要素を「線と箱を使って」まとめたものを箱ひげ図という
・「最小値、第1四分位数、中央値、第3四分位数、最大値」をもとに箱ひげ図をつくる
・箱ひげ図の両端を見れば、データの範囲が分かる