<ポイント>
・確率を求めるときは、まず「すべての場合の数」を求める
・書き出すときは「順序だてて」整理しながら書き出すこと
・図形の周りを点が移動するタイプは、場合分けして考える
【例題】
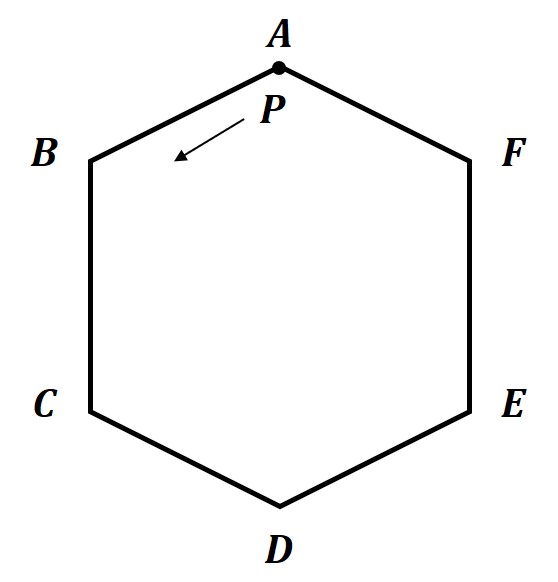
図のように正六角形ABCDEFGの周上を、点Pが移動します。点Pは頂点Aから出発し、さいころをふって出た目の数だけ正六角形の頂点の上を反時計回りに移動します。たとえば、3が出た場合はA→B→C→Dと移動します。
さいころを2回ふって、点Pが頂点Cにいる確率を求めなさい。
【解説】
まず、〔すべての場合の数〕を求めていきます。
さいころを2回ふるので、目の出方は全部で 6×6=36通りあります。
図のように正六角形ABCDEFGの周上を、点Pが移動します。点Pは頂点Aから出発し、さいころをふって出た目の数だけ正六角形の頂点の上を反時計回りに移動します。たとえば、3が出た場合はA→B→C→Dと移動します。
さいころを2回ふって、点Pが頂点Cにいる確率を求めなさい。

【解説】
まず、〔すべての場合の数〕を求めていきます。
さいころを2回ふるので、目の出方は全部で 6×6=36通りあります。
ここで、頂点Cにくるためには、出た目の和がいくらになればいいのかを考えると、
和が2, 8, 14, …になればいいことが分かります。
(実際に手でPを移動させながら考えます)
さいころを2回ふったときの目の和は最小で2, 最大で12なので、
(ⅰ)和が2になるとき(1周目でCにくる)
(ⅱ)和が8になるとき(2周目でCにくる)
の2つの場合を考えればよいことになります。
(ⅰ)和が2になるとき
(1回目にふったときの目, 2回目にふったときの目)とすると、
(1, 1)の場合だけなので、1通り
(ⅱ)和が8になるとき
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)の5通り
(ⅰ)(ⅱ)より、さいころを2回ふってPがCにくるのは、
1+5=6通り
よって、求める確率は 6/36=1/6 (答え)
<まとめ>
・確率を求めるときは、まず「すべての場合の数」を求める
・書き出すときは「順序だてて」整理しながら書き出すこと
・図形の周りを点が移動するタイプは、場合分けして考える
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

