<ポイント>
・確率を求めるときは、まず「すべての場合の数」を求める
・さいころに関する確率では、さいころを区別して考える
・2つのサイコロを投げた場合、「すべての場合の数は36通り」
2つのさいころを同時に投げるとき、次の確率を求めなさい。
① 出る目の数の和が 5 になる確率
② 出る目の数の和が 10以上になる確率
【解説】
「2つのさいころを投げる」場合は、2つのサイコロに名前をつけます。
今回は、さいころA,Bとします。
さいころは1〜6の目があり、それが2つあるため、
〔すべての場合の数〕=6×6=36通り
(こちらについては覚えておく方がいいです)
① 出る目の数の和が 5 になる確率
「出る目の数の和が 5 になる」のは、
(A, B)として表すと、
(1, 4), (2, 3)(3, 2)(4, 1)の4通り。
したがって、求める確率は 4/36=1/9 (答え)
② 出る目の数の和が10以上になる確率
和が10以上ということは、
(ⅰ)和が10の場合
(4, 6), (5, 5), (6, 4) の3通り
(ⅱ)和が11の場合
(5, 6), (6, 5) の2通り
(ⅲ)和が12の場合
(6, 6) の1通り
したがって、
〔和が10以上になる場合の数〕=3+2+1=6通り
よって、
求める確率は、6/36=1/6 (答え)
<補足>
さいころの和についての確率は、よく出題されます。
上の例題のように、問題で指示されたものだけ書き出してもいいですし、下の表をさっと書いて考えることもできます。
書くのに時間はかかりますが、見落としにくいという利点もあります。
自分に合った方法で構いませんので、練習しておきましょう。
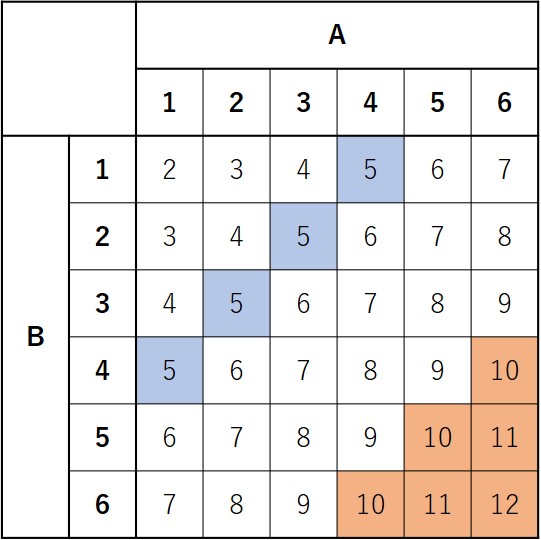
なお、①の問題に該当するものを青色に、②の問題に該当するものをオレンジ色にしています。
試験では色付けはできませんので、〇をつけるなど、工夫して使ってみてください。
<まとめ>
・確率を求めるときは、まず「すべての場合の数」を求める
・さいころに関する確率では、さいころを区別して考える
・2つのサイコロを投げた場合、「すべての場合の数は36通り」
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

