<ポイント>
・平行な2直線間の距離は、どこでも等しい
・「底辺が共通で、高さが等しい」ならば、三角形の面積は等しい
・「底辺に平行な直線上に頂点をとる」ならば、面積は変わらない
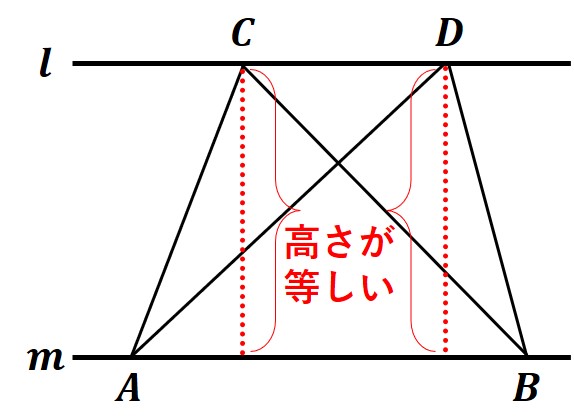
図にある直線 l, m は平行な直線があります。
2直線が平行であるならば、2直線間の距離は、どこでも等しくなります。
(逆に言えば、2直線間の距離が変わるのなら、それらの直線は平行ではない)
なお、「2直線間の距離」とは、
片方の直線上の点から、もう片方の直線へ下した垂線の長さのことです。
そのため、図にある△CABと△DABは「ABを底辺として見たとき、高さは同じ」になります。
「底辺が共通で、高さが等しい」ならば、三角形の面積は等しいと言えます。
([三角形の面積]=[底辺]×[高さ]×(1/2) で求めるため)
このことより、「底辺をABとしたまま、直線l上にC,D以外の点をとって三角形をつくった」としても、その面積は△CABと△DABと同じになるということです。
(このように、「面積を変えずに、三角形の形を変える」ことを、等積変形といいます)
<補足>
「△CABと△DABの面積が等しい」ことを、△CAB=△DABと表します。
三角形どうしを「=」で結ぶと、その面積が等しいことを表します。
(合同の記号「≡」と間違えないように注意)
<まとめ>
・平行な2直線間の距離は、どこでも等しい
・「底辺が共通で、高さが等しい」ならば、三角形の面積は等しい
・「底辺に平行な直線上に頂点をとる」ならば、面積は変わらない
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

