長方形やひし形、正方形がこれにあたり、
（平行四辺形の）特別な場合なので、平行四辺形の性質のすべてを持っています。

【平行四辺形の性質（定理）】　
①２組の対辺がそれぞれ等しい
②２組の対角はそれぞれ等しい
③対角線はそれぞれの中点で交わる
 
 
（２）長方形の定義と性質
長方形の定義：４つの角がすべて等しい（90°）四角形

その性質としては、定義・平行四辺形の性質に加えて、「（２本の）対角線の長さが等しい」というものがあります。
下の図で言えば、AC＝BDとなっています。

 
 
（３）ひし形の定義と性質
ひし形の定義：４つの辺がすべて等しい四角形

その性質としては、定義・平行四辺形の性質に加えて、「（２本の）対角線が垂直に交わる」というものがあります。
上の図で言えば、EG⊥FHとなっています。

＜補足＞

平行四辺形と、その特別な場合である長方形・ひし形・正方形は以下のような関係になっています。

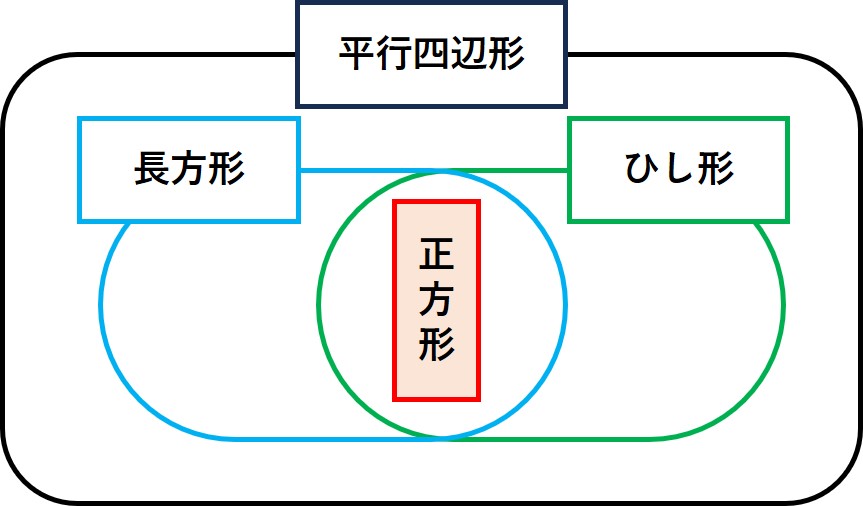
平行四辺形の特別な場合として、「長方形とひし形」があり、
それら２つの性質を合わせ持つものが「正方形」ということです。

＜まとめ＞

・長方形・ひし形は平行四辺形（のなかま）である
・長方形の定義：４つの角がすべて等しい（90°）四角形
・ひし形の定義：４つの辺がすべて等しい四角形