＜ポイント＞
・証明をしていくとき、「共通な角」を使うことがある
・角の大きさが正確に分からなくても、「共通な角」で表すことができればOK
・直角三角形の合同条件：「斜辺と１つの鋭角がそれぞれ等しい」「斜辺と他の１辺がそれぞれ等しい」
【問題】
図のように、直角二等辺三角形ABCの頂点Aを通る直線lに、頂点B,Cからそれぞれ垂線をひき、交点をD,Eとします。このとき、BD＋CE＝DEとなることを証明しなさい。
【方針】
直角以外の角の大きさは分からないけど、「三角形の内角の和は180°となる」こと、「直線まわりの角の大きさは180°である」ことを利用すれば、角の大きさが等しいといえる場合が多い。
その場合は、「２つの角を、共通な角を使って表す」ことを目指す。
【証明】
△DABと△ECAにおいて、
仮定より、
∠ADB＝∠CEA＝90°…①
AB＝CA…②
図のように、直角二等辺三角形ABCの頂点Aを通る直線lに、頂点B,Cからそれぞれ垂線をひき、交点をD,Eとします。このとき、BD＋CE＝DEとなることを証明しなさい。
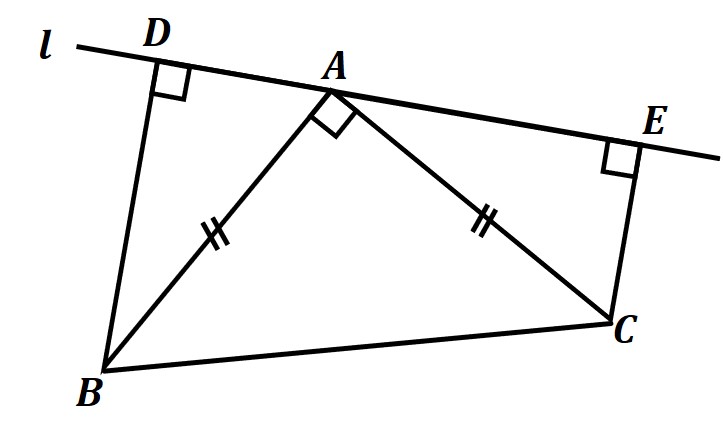
【方針】
直角以外の角の大きさは分からないけど、「三角形の内角の和は180°となる」こと、「直線まわりの角の大きさは180°である」ことを利用すれば、角の大きさが等しいといえる場合が多い。
その場合は、「２つの角を、共通な角を使って表す」ことを目指す。
【証明】
△DABと△ECAにおいて、
仮定より、
∠ADB＝∠CEA＝90°…①
AB＝CA…②
また、
∠ABD＝180°－(∠ADB＋∠DAB)＝90°－∠DAB
（補足：△DABの内角の和が180°であることを利用）
∠CAE＝180°－(∠BAC＋∠DAB)＝90°－∠DAB
（補足：直線まわりの角が180°であることを利用）
よって、∠ABD＝∠CAE…③ （←∠ABDも∠CAEも、同じ 90°－∠DAB で表せたので）
①,②,③より、直角三角形の斜辺と１つの鋭角がそれぞれ等しいので、
△DAB ≡ △ECA
合同な図形の対応する辺は等しいので、BD＝AE, AD＝CE
したがって、BD＋CE＝AE＋AD＝DE （証明終わり）
＜補足＞
上の図のように、直角三角形を使って合同（や相似）を考えるときには、直角以外の２つの鋭角を〇と×で表すことがあります。
これは、三角形の内角の和が180°で、直角を除いた「〇＋×＝90°」となって、（〇や×と）等しい角ができることが多いためです。
それぞれの角の大きさは分からないけど、その「和が一定である」ため、非常に便利なのでぜひ使ってみてください。
＜まとめ＞
・証明をしていくとき、「共通な角」を使うことがある
・角の大きさが正確に分からなくても、「共通な角」で表すことができればOK
・直角三角形の合同条件：「斜辺と１つの鋭角がそれぞれ等しい」「斜辺と他の１辺がそれぞれ等しい」
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
