<ポイント>
・〔n角形の内角の和〕=180°×(n−2)
・〔多角形の外角の和〕=360°
・〔正多角形の1つの内角〕=180°×{(n−2)/n}
どのような多角形であっても、内角の和は以下の公式から求めることができます。
〔n角形の内角の和〕=180°×(n−2)
たとえば、五角形の内角の和であれば、n=5を代入して、
180°×(5−2)=180°×3=540°
と求めることができます。
また、この公式にある (n−2) の部分は「その多角形がいくつの三角形に分けられるか」を表しています。
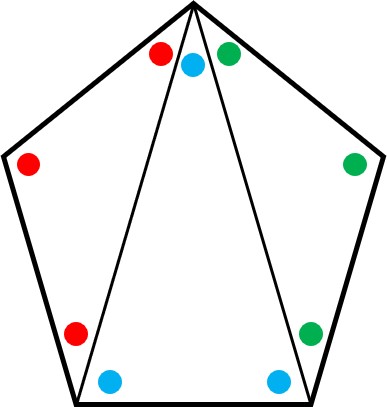
五角形の場合は「1つの頂点から、2本の対角線を引くことができる」ので、中に三角形が3つできます。
そして、各三角形の内角の和が180°であることから、180°をかけているのです。
(2)外角の和
多角形であれば、「何角形であっても」外角の和は 360° となります。
どんな多角形であっても、ひとつの頂点における「[内角]+[外角]=180°」という関係があります。
これがその多角形の頂点の数だけあるので、180°・n の角度がある。
そこから、〔内角の和〕をひくと、
〔n角形の外角の和〕=180°・n−180°・(n−2)=360° となります。
(nに何を代入しても同じになる)
(3)正多角形の1つの内角
正多角形の1つの内角の大きさは、〔正n角形の内角の和〕÷〔頂点の数 n〕で求めることができるので、
〔正多角形の1つの内角〕=180°×{(n−2)/n}
という公式で求めることができます。
(「全部を求めて、1つあたりを求める」というイメージ)
<まとめ>
・〔n角形の内角の和〕=180°×(n−2)
・〔多角形の外角の和〕=360°
・〔正多角形の1つの内角〕=180°×{(n−2)/n}
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

