<ポイント>
・図形を折り返してできる角は「もどしたときに、どの角と重なるか」を考える
・同じ大きさになる角には、◯や●など同じ印を入れておくと分かりやすい
・「折り返す前の図形が平行」であれば、それらの辺は折り返したあとも平行となる
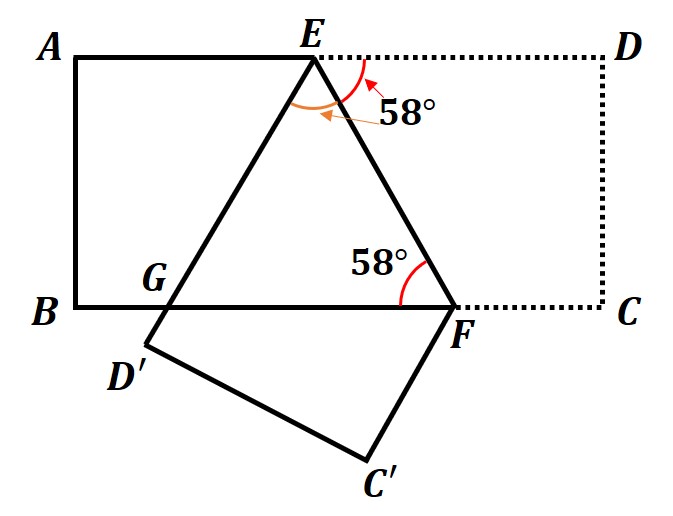
長方形ABCDを図のように、EFを折り目として折り返した。このとき、次の問いに答えなさい。
(1)∠AEGの大きさを求めなさい。
(2)∠BGEの大きさを求めなさい。

【解説】
(1)∠AEGの大きさを求めなさい。
四角形ABCDは長方形なので、AD//BCとなっています。
平行な直線では錯角は等しいので、
∠EFG=∠DEF=58°
また、「∠DEFを折り返すと、∠GEFとなる」ので、
∠DEF=∠GEF=58°
よって、
∠AEG=180°−(∠DEF+∠GEF)=180°−116°=64°
このように、図形を折り返してできる角は「もどしたときに、どの角と重なるか」を考えることが大切です。これを利用するために、同じ大きさになる角には、◯や●など同じ印を入れておくと分かりやすいのでおすすめです。
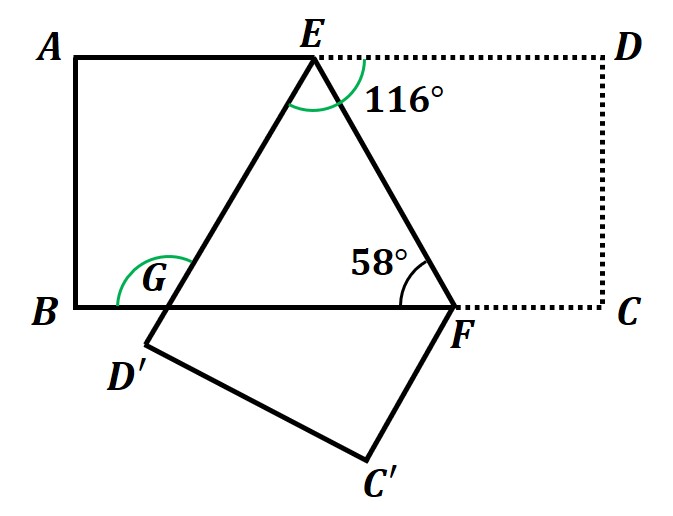
(2)∠BGEの大きさを求めなさい。
四角形ABCDは長方形なので、AD//BCとなっています。
平行な直線では錯角は等しいので、
∠DEG=∠BGE=58°×2=116°
<まとめ>
・図形を折り返してできる角は「もどしたときに、どの角と重なるか」を考える
・同じ大きさになる角には、◯や●など同じ印を入れておくと分かりやすい
・「折り返す前の図形が平行」であれば、それらの辺は折り返したあとも平行となる
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

