<ポイント>
・直線が交わっているとき、「向かい合っている角」を対頂角という
・対頂角はどんな場合も等しい
・3本の直線が2点で交わっているとき、同位角と錯角ができる
(1)対頂角
2つの直線が交わっているとき、「向かい合っている角」を対頂角といいます。
この対頂角は、どんな場合であったとしても、等しくなっています。
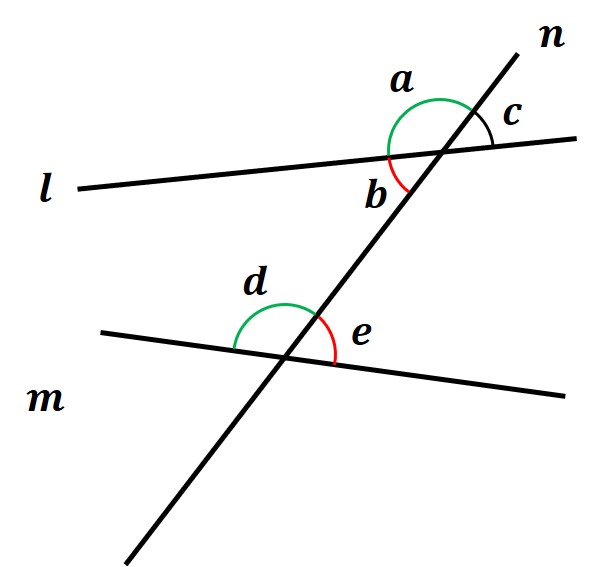
この図の場合、「∠b と∠c」が対頂角の関係になっており、その大きさは等しい。
つまり、∠b=∠c ということです。
(2)同位角
上図の2つの直線 l, m に対して、1つの直線 n が交わってできる角のうち、
「∠a と∠d の位置関係」にあるものを同位角といいます。
(∠c と∠e も同位角となる)
2つの直線が交わっているとき、「向かい合っている角」を対頂角といいます。
この対頂角は、どんな場合であったとしても、等しくなっています。

この図の場合、「∠b と∠c」が対頂角の関係になっており、その大きさは等しい。
つまり、∠b=∠c ということです。
(2)同位角
上図の2つの直線 l, m に対して、1つの直線 n が交わってできる角のうち、
「∠a と∠d の位置関係」にあるものを同位角といいます。
(∠c と∠e も同位角となる)
これらの角(∠a と∠d)は、「2つの交点において左上にある角」です。
このように、同じような位置関係にある角を同位角といいます。
(3)錯角
上図の2つの直線 l, m に対して、1つの直線 n が交わってできる角のうち、
「∠b と∠e の位置関係」にあるものを錯角といいます。
これらの角(∠b と∠e)は、「2つの交点を通る Z のような形でできる角」です。
このような位置関係にある角を錯角といいます。
<補足>
下図のように、2つの直線 lとm が平行である場合、同位角と錯角の大きさはそれぞれ等しくなっています。
同位角:∠a = ∠c
錯角:∠b = ∠c
このように、平行な直線がある場合は「同位角と錯角に注目して」、問題を解き進めます。

<まとめ>
・直線が交わっているとき、「向かい合っている角」を対頂角という
・対頂角はどんな場合も等しい
・3本の直線が2点で交わっているとき、同位角と錯角ができる
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

