たとえば、1次関数の式を答えるもので、
①「グラフの傾きが 2 で点(3, 9)を通る」という問題であれば、
a＝2 を代入して、y＝2x＋b と考えます。

そして、これが (3, 9) を通る ので、x＝3, y＝9 を代入
2・3＋b＝9
b＝3

よって、求める式は y＝2x＋3

②「変化の割合が －3 で点(2, －4)を通る」という問題であれば、
a＝－3 を代入して、y＝－3x＋b と考えます。

そして、これが (2, －4) を通る ので、x＝2, y＝－4 を代入
－3・2＋b＝－4
b＝2

よって、求める式は y＝－3x＋2
というように考えます。
 
 
（２）「y＝〇x＋● のグラフに平行」パターン
1次関数のグラフが平行であれば、それらの傾きが等しいと考えることができます。
「y＝〇x＋● のグラフに平行」ということなら、求める式の傾きも〇となります。

たとえば、1次関数の式を答えるもので、
①「y＝2x＋2 のグラフに平行で、点(1, 0)を通る」という問題であれば、
「平行なら、傾きが等しい」ので、a＝2 を代入して、y＝2x＋b と考えます。

そして、これが (1, 0) を通る ので、x＝1, y＝0 を代入
2・1＋b＝0
b＝－2

よって、求める式は y＝2x－2

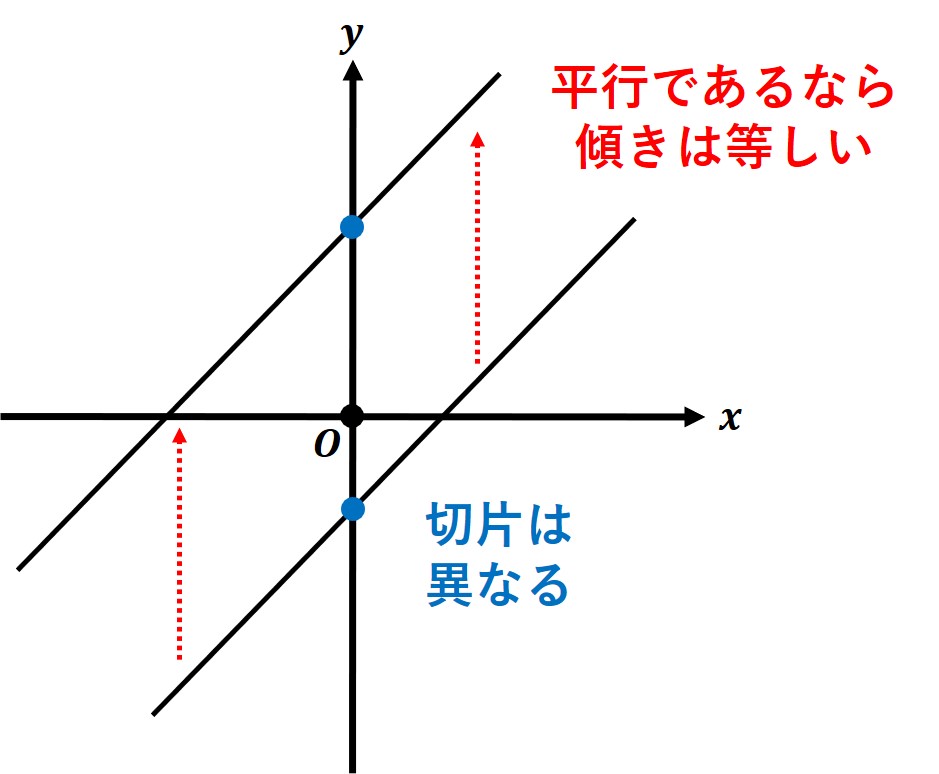
なお、上記のような問題では、「平行である」としか言っていませんので、元となる式の切片部分は無視することになります。
「平行なら、傾きが等しい」という部分のみを利用します。

＜まとめ＞

・「グラフの傾き」「変化の割合」が与えられたら、aに代入する（y＝ax＋b）
・グラフが通る点の座標が分かれば、式 y＝ax＋b に代入する
・1次関数のグラフが平行であれば、傾きが等しい