たとえば、y＝2x＋1について、考えます。

こちらの一次関数において、
① x＝3からx＝5まで増加したときの変化の割合
② x＝4からx＝10まで増加したときの変化の割合
を比べてみます。

①x＝3からx＝5まで増加したときの変化の割合
まずは、x＝3とx＝5に対応するyの値を、それぞれ求めておきます。
x＝3のとき、y＝2・3＋1＝7
x＝5のとき、y＝2・5＋1＝11

これを用いて、〔変化の割合〕＝〔yの増加量〕/〔xの増加量〕を考えると、
〔xの増加量〕＝5－3＝2
〔yの増加量〕＝11－7＝4
よって、〔変化の割合〕＝4/2＝2

②x＝4からx＝10まで増加したときの変化の割合
まずは、x＝3とx＝5に対応するyの値を、それぞれ求めておきます。
x＝4のとき、y＝2・4＋1＝9
x＝10のとき、y＝2・10＋1＝21

これを用いて、〔変化の割合〕＝〔yの増加量〕/〔xの増加量〕を考えると、
〔xの増加量〕＝10－4＝6
〔yの増加量〕＝21－9＝12
よって、〔変化の割合〕＝12/6＝2

よって、①、②どちらの区間で考えても、〔変化の割合〕＝2となります。
他の区間で測っても同じになりますので、「変化の割合は一定である」といえます。
 
 
（２）変化の割合は a に等しい
一次関数 y＝ax＋b の変化の割合は a に等しいといえます。

上記の例でも、y＝2x＋1 に考えているので、a＝2
これをもとに考えた変化の割合が2 ですので、「aに等しくなっている」とわかります。

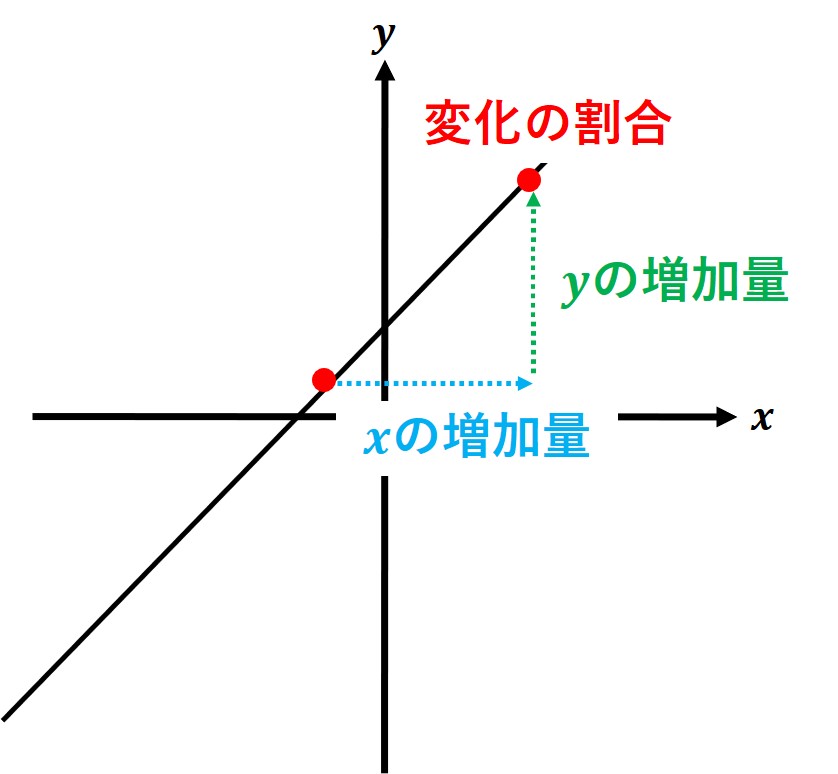
（３）変化の割合から分かること
一次関数 y＝ax＋b において、「a と変化の割合が等しい」ことから、次のことが言えます。

・a＞0 ならば「xが増加すると、yも増加する」
・a＜0 ならば「xが増加すると、yは減少する」

a＝〔変化の割合〕＝〔yの増加量〕/〔xの増加量〕なので、

〔xの増加量〕が正で、
〔yの増加量〕が正なら〔変化の割合〕も正
〔yの増加量〕が負なら〔変化の割合〕も負

となります。

＜補足＞

「一次関数 y＝ax＋b の変化の割合は a に等しい」のですが、この a について「xの値が1だけ増加したときのyの増加量である」ともいえます。

xの増加量が1のとき、
a＝〔変化の割合〕＝〔yの増加量〕/ 1＝〔yの増加量〕
つまり、a＝〔yの増加量〕（xの増加量が1のとき）

＜まとめ＞

・一次関数 y＝ax＋b の変化の割合は一定となる
・一次関数 y＝ax＋b の変化の割合は a に等しい
・一次関数 y＝ax＋b において、a＞0 ならば「xが増加すると、yも増加する」