<ポイント>
・基準となるものを n としておく
・問題の指示に従って計算を進める
・カレンダーで縦に並ぶ数字は「7ずつ増える」
〔問題〕
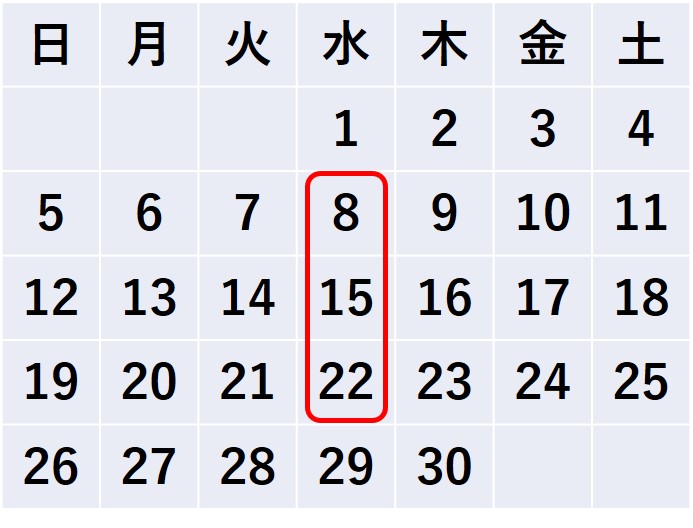
図はある月のカレンダーです。赤い線で囲まれた3つの数 8, 15, 22 の和は 45 で、真ん中の数 15 の 3倍になっている。このように、カレンダーにおいて縦に並んだ3つの数の和は、真ん中の数の3倍になる。このことを説明しなさい。
〔解答〕
図はある月のカレンダーです。赤い線で囲まれた3つの数 8, 15, 22 の和は 45 で、真ん中の数 15 の 3倍になっている。このように、カレンダーにおいて縦に並んだ3つの数の和は、真ん中の数の3倍になる。このことを説明しなさい。

〔解答〕
縦に並んだ3つの数のうち、真ん中の数を n とする。
そうすると、並んだ3つの数は n-7, n, n+7 と表せる。
これらの数の和は、
(n-7)+n+(n+7)=3n
よって、カレンダー上で縦に並んだ3つの数の和は、真ん中の数の3倍になる。
〔解説〕
まずは、基準となる「真ん中の数を n とする」ことから始めます。
そして、問題の材料となる「縦に並ぶ3つの数」を n を使って表します。
このとき、カレンダーで縦に並ぶ数字は「7ずつ増える」ということを利用しましょう。
ここまでくれば、この3つの数 n-7, n, n+7 を使って、問題の指示に沿った計算を進めて、
結論である「カレンダーにおいて縦に並んだ3つの数の和は、真ん中の数の3倍になる(=3n)」となるようにしていきます。
「説明しなさい。」という問題では、必ず「結論の式になるように問題を設定している」ので、結論に近づくように計算を進めましょう。
<まとめ>
・基準となるものを n としておく
・問題の指示に従って計算を進める
・カレンダーで縦に並ぶ数字は「7ずつ増える」
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

