<ポイント>
・〔転がる円すいの底面の円周〕×〔回転数〕=〔円Oの円周〕
・〔円Oの円周〕=〔母線の長さを半径とする円の円周〕
・〔円すいの側面積〕=〔母線〕・〔底面の半径〕・π
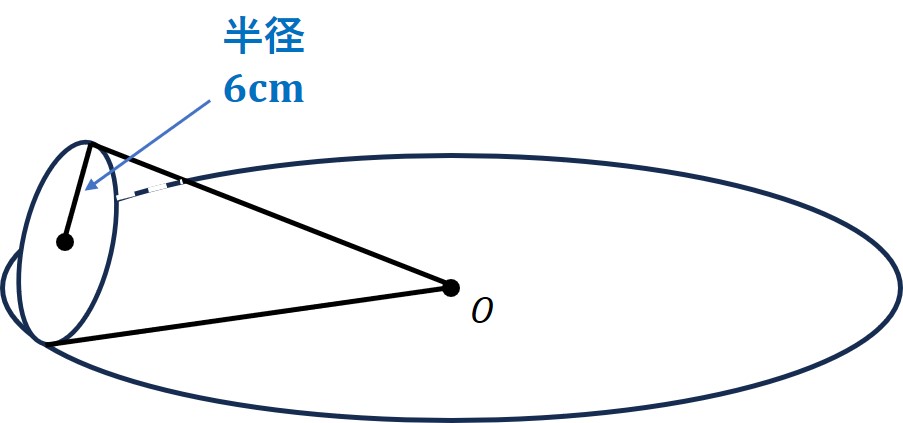
図のように、底面の半径が6cmの円すいを、点Oを中心として平面上で転がしたところ、図に示した円O上を1周して元の位置に戻るまでに、2回転半した。このとき、次の問いに答えなさい。
(1)円すいの母線の長さを求めなさい。
(2)円すいの表面積を求めなさい。
〔解説〕
(1)円すいの母線の長さを求めなさい。
半径6cmの円(底面の円)が2回転半するまでに、この底面の円が通った道のりは、
〔転がる円すいの底面の円周〕×〔回転数〕=〔円Oの円周〕より、
「〔半径6cmの円の円周〕× 2.5=12π・2.5=30π cm
これが〔円Oの円周の長さ〕となるため、
〔円Oの半径 r (=母線の長さ)〕×2×π=30π (円周=直径×π)
2πr=30π
r=15 つまり、「母線の長さ 15cm」ということになります。
(2)円すいの表面積を求めなさい。
〔円すいの表面積〕=〔底面積〕+〔側面積〕より、
〔底面積〕=πr2=π・62=36π
〔側面積〕=〔母線〕・〔底面の半径〕・π=15・6・π=90π
したがって、
〔円すいの表面積〕=36π+90π=126π cm2
<まとめ>
・〔転がる円すいの底面の円周〕×〔回転数〕=〔円Oの円周〕
・〔円Oの円周〕=〔母線の長さを半径とする円の円周〕
・〔円すいの側面積〕=〔母線〕・〔底面の半径〕・π
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

