<ポイント>
・〔角柱の体積 V〕=〔底面積 S〕×〔高さ h〕
・〔円柱の体積 V〕=〔底面積 S〕×〔高さ h〕=〔πr2〕×〔高さ h〕
・高さは「底面に対して垂直な直線」となっている
(1)角柱の体積
角柱(多角形を底面にもつ柱体)の体積は、
〔角柱の体積 V〕=〔底面積 S〕×〔高さ h〕
という公式で求めることができます。
(このとき、高さhは必ず底面に対して垂直になっている)
角柱(多角形を底面にもつ柱体)の体積は、
〔角柱の体積 V〕=〔底面積 S〕×〔高さ h〕
という公式で求めることができます。
(このとき、高さhは必ず底面に対して垂直になっている)
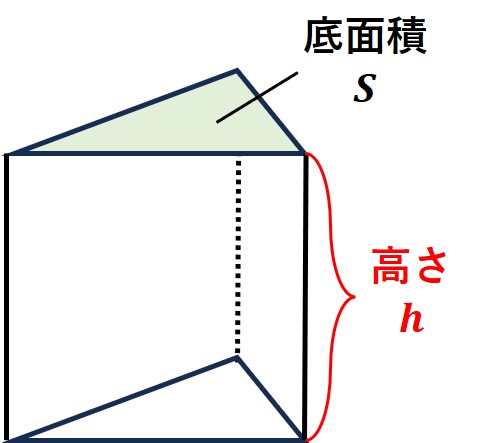
図のような三角柱の体積であれば、
〔角柱の体積 V〕=〔底面の三角形の面積 S〕×〔高さ h〕
という式で求めていきます。
(2)円柱の体積
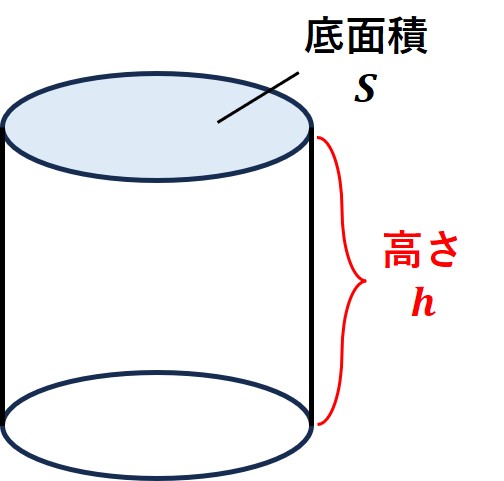
円柱の体積は、
〔円柱の体積 V〕=〔底面積(円) S〕×〔高さ h〕=〔πr2〕×〔高さ h〕
という公式で求めることができます。
(このとき、高さhは必ず底面に対して垂直になっている)
〔例題〕
① 底面が一辺3cmの正方形で、高さ5cmの直方体(四角柱)の体積を求めなさい。
〔角柱の体積 V〕=〔底面積 S〕×〔高さ h〕より、
3・3・5=45cm3
② 底面が半径5cmの円で、高さ6cmの円柱の体積を求めなさい。
〔円柱の体積 V〕=〔底面積 S〕×〔高さ h〕=〔πr2〕×〔高さ h〕より、
52π・6=25π・6=150π cm3
<まとめ>
・〔角柱の体積 V〕=〔底面積 S〕×〔高さ h〕
・〔円柱の体積 V〕=〔底面積 S〕×〔高さ h〕=〔πr2〕×〔高さ h〕
・高さは「底面に対して垂直な直線」となっている
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

