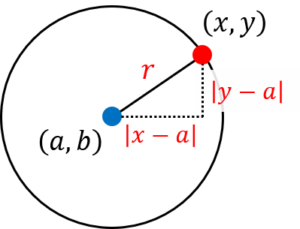| 〔質問〕 円の方程式はなぜ (x-a)2+(y-b)2=r2 の形式になるのですか? |
| 〔回答〕 シンプルに、三平方の定理によるものです。 円上の点ということは「中心との距離=半径」ですので、下図のような直角三角形ができることになります。
そのため、正確には |x-a|2+|y-b|2=r2 という式を立てることができ、 |
〔補足〕
なお、厳密には、三平方の定理は直角三角形に対してしか適用できませんので、次の赤の4点に関しては同じようにして考えることができません。
なお、厳密には、三平方の定理は直角三角形に対してしか適用できませんので、次の赤の4点に関しては同じようにして考えることができません。
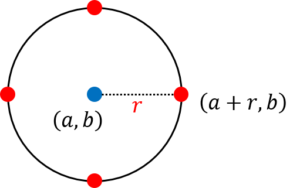
ただ、例えば、右側の点であれば、実際の座標は (a+r, b) ですので(中心に対して、x座標だけがr大きいため)、(x-a)2+(y-b)2=r2 の式を満たすような x, y になっています。
他の4点も同様のことが言えますので、よって、この4点のことも含めて、(x-a)2+(y-b)2=r2 で一本化できる、という理屈です。
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |