<ポイント>
・文章題では「問われている未知数を x,y を使って表す」のが基本
・「通過に関する問題」では、状況を整理する図を描く
・「橋を渡り始めてから、渡り終える」までに進む距離は、[橋の長さ]+[列車の長さ]
【問題】
ある列車が、1280mの鉄橋を渡り始めてから渡り終えるまでに60秒かかりました。同じ列車が、2030mのトンネルに入り始めてから完全に出るまでに90秒かかりました。このときの列車の長さと速さを求めなさい。
【解説】
まず、文章題では「問われている未知数を x,y を使って表す」のが基本なので、
列車の長さを x m、列車の速さを秒速 y mとします。
問題文には、
・1280mの鉄橋を渡り始めてから渡り終えるまでに60秒かかった…①
・2030mのトンネルに入り始めてから完全に出るまでに90秒かかった…②
と書いてあります。
①のようすを図に示すと、このようになります。
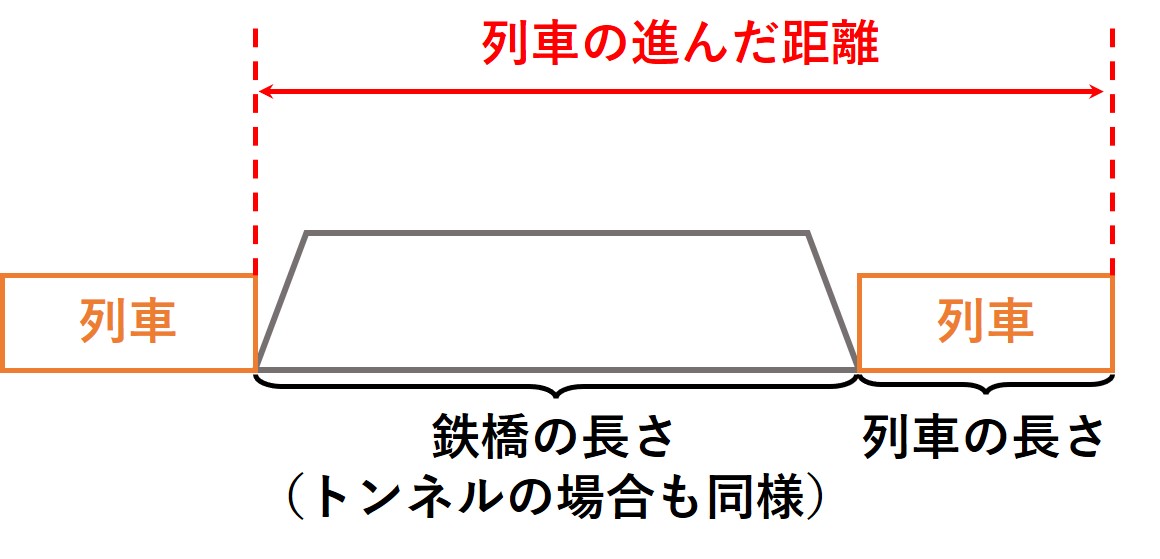
これを使って式を立てると、
・1280mの鉄橋を渡り始めてから渡り終えるまでに60秒かかった
⇒ [鉄橋の長さ]+[列車の長さ]=[列車が60秒で進んだ距離]
⇒ 1280m+x m=y m/s・60s
⇒ 1280+x=60y …①
上の図を参考に②についても式を立てると、
・2030mのトンネルに入り始めてから完全に出るまでに90秒かかった
⇒ [トンネルの長さ]+[列車の長さ]=[列車が90秒で進んだ距離]
⇒ 2030m+x m=y m/s・90s
⇒ 2030+x=90y …②
1280+x=60y …①
2030+x=90y …②
このように、①, ②の式を立てることができたので、連立方程式を解くと、
x=220, y=25
つまり、
「列車の長さが 220m、列車の速さが秒速 25m」ということになり、
これらは「問題に適している」。
〔答え〕列車の長さ… 220m、列車の速さ…秒速 25m
<補足>
列車などの乗り物が、鉄橋やトンネルなどを通過する問題では、「その乗り物の先頭部分が、どこからどこまで動いたのか」を考えます。
つまり、「先頭に注目して動きを図に表す」ことができれば、式を立てやすいということです。
移動前後で、乗り物の先頭に注目、一番後ろに注目など変えないようにしましょう。
<まとめ>
・文章題では「問われている未知数を x,y を使って表す」のが基本
・「通過に関する問題」では、状況を整理する図を描く
・「橋を渡り始めてから、渡り終える」までに進む距離は、[橋の長さ]+[列車の長さ]
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

