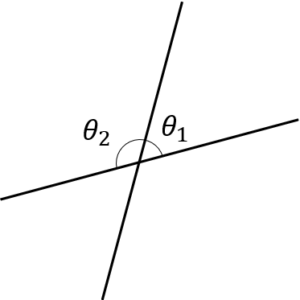
〔質問〕

ベクトルaに平行な直線をl、ベクトルbに平行な直線をmとするとき、lと mのなす角をαとするときcosαを求めよ。という問題で、ベクトルaとbのなす角をθとして考えるとき、θが鈍角、鋭角になる場合で答えが変わってくるのですか？また、鈍角か鋭角かはどうしたらわかるのですか？

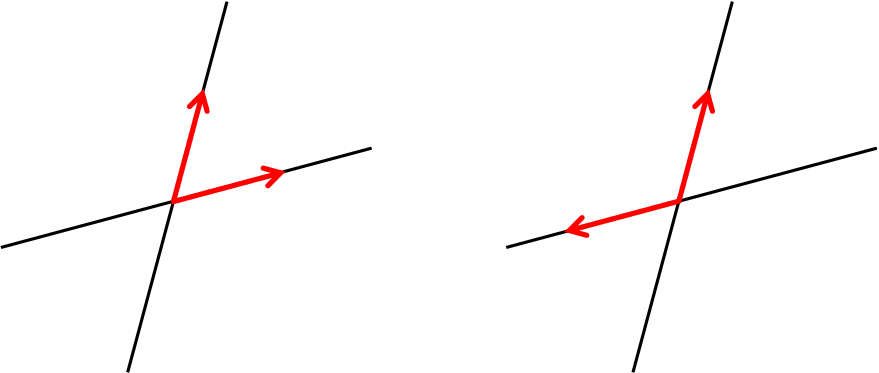
〔回答〕

例えば下図のようなケースの場合、θ₁ と θ₂ の両方ともが「２直線のなす角」に相当します。
そのため、問題文には「鋭角の方を求めよ」のような指定がありますので、それに従って θ₁ 側を答える、というようにします。
もし、cos が －1/2 となって、つまり 120° だった、となれば、その場合は単純に 180° から差し引いて 60° と答えれば大丈夫です。

次に、計算上、どちら側が求まるのか、ですが、これは計算してみないとわかりません。
というのも、最初にベクトルを定める際に、向きまでを考慮した定め方をしていないでしょうから（下図の違いまでを考慮していない）、
あくまでも事後的に、「内積から得られた cos の値の正負によって、鋭角側だったのか鈍角側だったのかがわかる」というものです。