<ポイント>
・頂点O, OA, OB でつくる角を∠AOBと表す
・「一直線の角の大きさ」=180°
・対頂角は等しい
図のように、

頂点O, 辺OA, 辺OB でつくる角を∠AOBと表します。(∠は「角」を表す記号)
「OからAとBを結んだときに、頂点Oの位置にできる角度」というイメージです。
そのため、∠BOAの場合でも、同じ角度(の大きさ)を表すことになります。
(∠AOB=∠BOAということ)
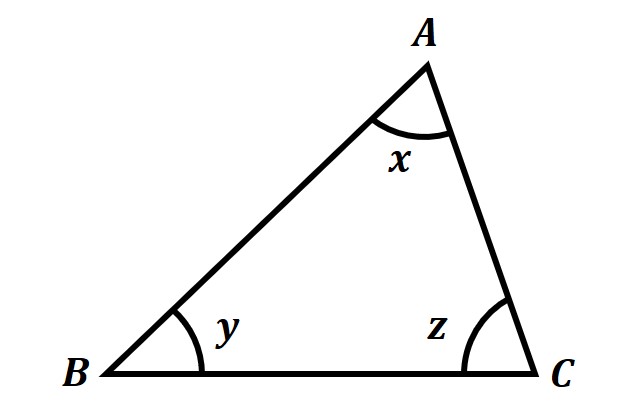
こちらの△ABCの角x, y, zであれば、以下のように表すことができます。
(それぞれの角は、いずれの形で表しても、同じ部分の角を表す)
∠A=∠x=∠BAC=∠CAB
∠B=∠y=∠ABC=∠CAB
∠C=∠z=∠BCA=∠ACB
(2)角の大きさ
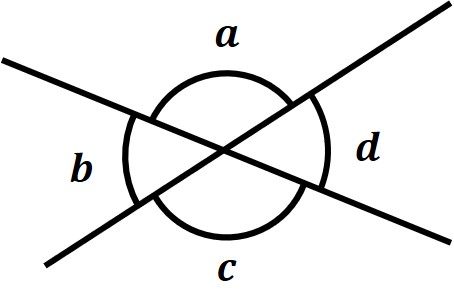
・一直線分の角の大きさ
「一直線分の角度」は180°になります。
この図の場合だと、
∠a+∠b=∠a+∠d=180° ということです。
他にも、∠b+∠a=∠b+∠c=180° といえます。
・対頂角
「向かい合う角」のことを対頂角といいます。
この図の場合だと、「∠aと∠c」「∠bと∠d」がそれぞれ対頂角となります。
そして、対頂角は等しいので、「∠a=∠c」「∠b=∠d」という関係になっています。
<補足>
1回転分の角度は360°で、この角度がすべての基本となっています。
1直線分だと、ちょうどこの半分になるため、360°÷2=180°と考えるわけです。
<まとめ>
・頂点O, OA, OB でつくる角を∠AOBと表す
・「一直線の角の大きさ」=180°
・対頂角は等しい
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

