この角（∠AOB）の二等分線の作図の方法は、以下の手順となります。

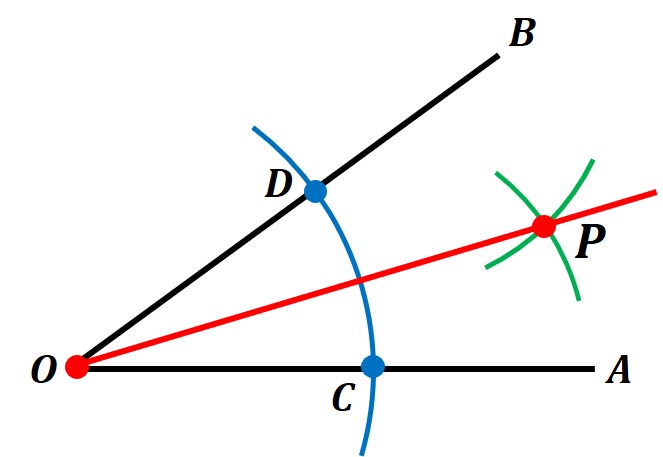
① 点Oを中心とする適当な円弧（青色）を描き、その交点をC, Dとする
② 点C, Dを中心とする「等しい半径の円弧（緑色）」を描き、その交点をPとする
③ 点Oと点Pを結ぶ（赤色）

この直線OPが「∠AOBの二等分線」となります。
 
 
（２）角の二等分線の性質
角の二等分線上の点は、どこの点でも（その角をつくる）線分までの距離が等しくなっています。

上の図において、
〔Pと線分OAの距離〕＝〔Pと線分OBの距離〕 であるということです。
（角の二等分線上に他に点をとったとしても、辺OA,OBまでの距離は等しくなります）

＜補足＞

三角形の「3つの角の二等分線の交点」を中心として、三角形の内接円をつくることができます。

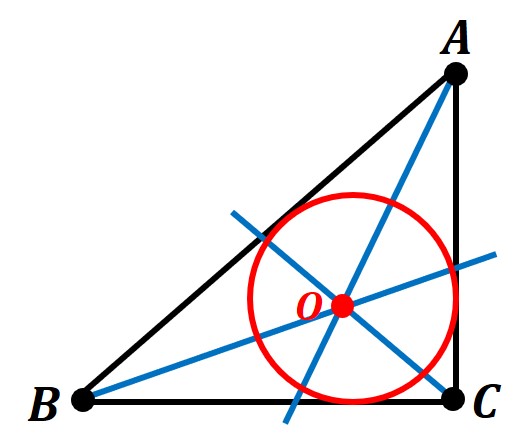
下の図は、△ABCの内接円（赤い円）を表しています。

それぞれの角（∠A,∠B,∠C）の二等分線を描き、その交点Oとします。
この交点Oが内接円の中心となり、各辺に接する円を描くことができます。
（なお、半径をつくるためには、点Oからいずれかの辺に垂線をつくり、それを使う）
これは「角の二等分線上の点は、どこでもその角をつくる線分までの距離が等しい」という性質を利用しています。

＜まとめ＞

・「角度を二等分する直線」を角の二等分線という
・角の二等分線上の点は、どこの点でも（その角をつくる）線分までの距離が等しい
・三角形のそれぞれの角の二等分線の交点は「内接円の中心」となる