・数直線上で「ある数を表す点と原点との距離」を、その数の絶対値という
・正の数どうしでは、「絶対値の大きい数」の方が大きい
・負の数どうしでは、「絶対値の大きい数」の方が小さい
数直線上で「ある数を表す点と原点との距離」を、その数の絶対値といいます。
つまり、「絶対値は(数直線上における)距離」なので、+や−という符号はつかないことになります。
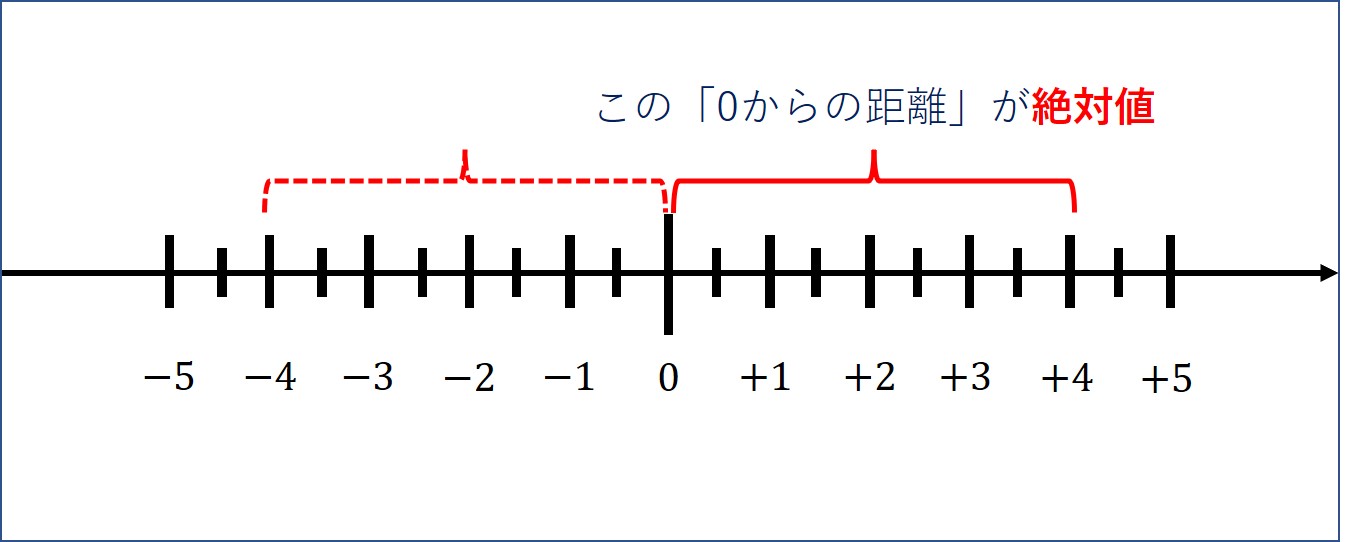
上の数直線を使って絶対値を考えると、
「+4」の絶対値は「0から4離れている」ので、4 となります。
同様に、「-4」の絶対値は「0から4離れている」ので、4 となります。
よって、符号が異なるだけの +4 と -4 の絶対値は(同じ)4 となることが分かります。
つまり、「符号が逆になっているだけなら、絶対値は等しくなる」ということが言えるのです。
〔例題1〕次の数の絶対値を求めなさい。
① +5 → 0 と +5 の距離は 5 なので、絶対値は「5」
② -3 → 0 と -3 の距離は 3 なので、絶対値は「3」
③ +(1/2) → 0 と +(1/2) の距離は 1/2 なので、絶対値は「1/2」
④ -4.3 → 0 と -4.3 の距離は 4.3 なので、絶対値は「4.3」
となります。
(簡単に言えば、「+や−を無視した数」が答えになります)
(2)絶対値と数の大小関係
・正の数どうしでは、「絶対値の大きい数」の方が大きい(数直線上で右側にある)
・負の数どうしでは、「絶対値の大きい数」の方が小さい(数直線上で左側にある)
という関係になっています。
数直線をイメージすると分かることですので、実際に書かなくてもよいので、頭の中に思い浮かべることができるようにしておきましょう。
絶対値には記号があって、「+〇 の絶対値」は、| 〇 | と表します。
例えば、
+12 の絶対値は |+12| と表し、|+12| = 12 となります。
・数直線上で「ある数を表す点と原点との距離」を、その数の絶対値という
・正の数どうしでは、「絶対値の大きい数」の方が大きい
・負の数どうしでは、「絶対値の大きい数」の方が小さい
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

