| 〔質問〕 中2の数学です。 「図形の調べ方」という単元で、ある問題が分かりません。 問)内角の和が次のようになるのは何角形ですか。 1)720° 答えにはこのように書かれています。 解説)180°×(n−2)=1080° n−2=4 n=6 答え、六角形 なぜ「n−2=4」になるのかと「n=6」になるのかが分からないです。教えてください。 |
| 〔回答〕 一般に、多角形の内角の和は、180°×(辺の数-2) になります。 これは、次の図のように、どこか1つの頂点から補助線(黄色)を引けば複数の三角形に分割して考えることができるためで、 例えば、六角形の場合には4つの三角形に分割されるため、「180°が4つ」というような計算をできることになるためです。 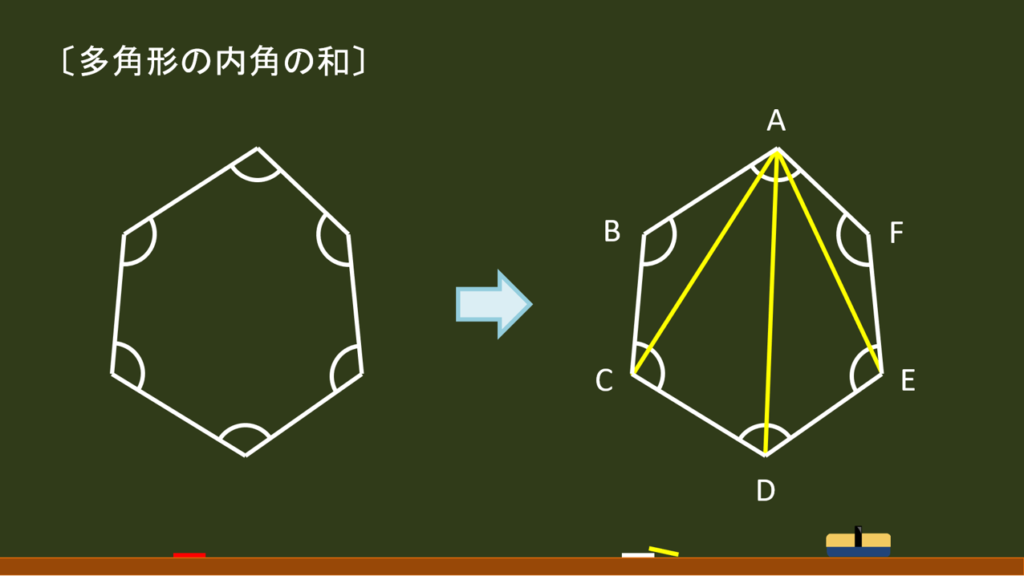 必ず「-2」となる理由ですが、 この図のケースだと、「△ABC, △ACD, △ADE, △AEF の個数」は「辺BC, 辺CD, 辺DE, 辺EF の数」と見ることができますので(△A●■ について、辺●■(点Aを含まない辺)を代表者と見立てて、その数を数えればいい)、 新たにできる三角形の個数は「6つの辺から、辺ABと辺AF(点Aを含む2つの辺)を除いた数に等しい」という考え方をすることができます。 そのため、「辺の数-2」個の三角形ができることになります。 方程式自体は、180(x-2)=1080 を解くのと同じ要領でよく、 |
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

