| 〔質問〕 関数f(x)=x4+4x3+2ax2 が極大値と極小値を持つ時aの範囲を求めよ、と言う問題なのですが、解説に x2+3x+a=0 が x=0以外と異なる解を持てばいいと書いてあったのですが、なぜ x=0はダメなのですか? |
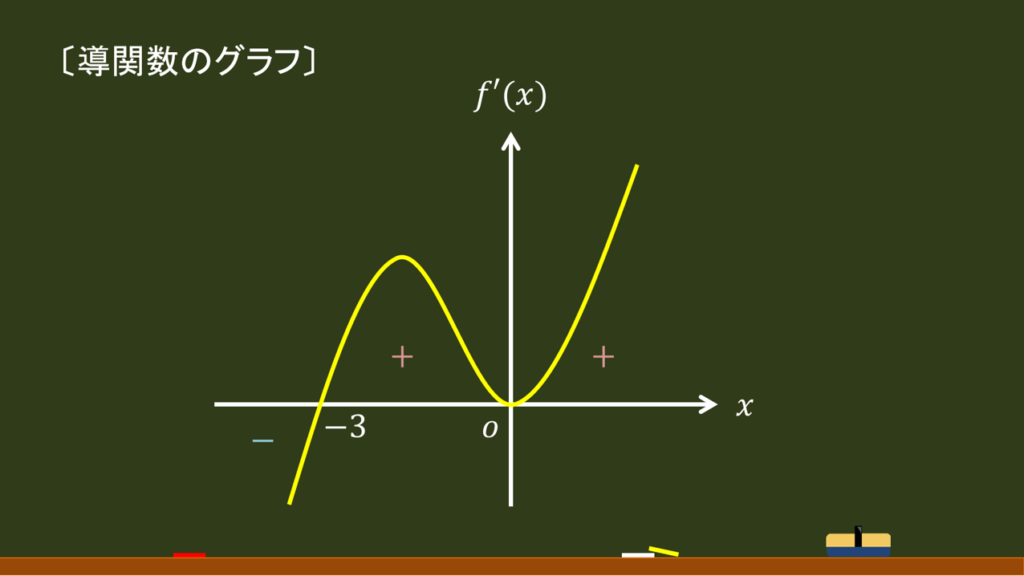
| 〔回答〕 「極大」は「導関数が正から負に切り替わる箇所」、「極小」は「導関数が負から正に切り替わる箇所」というのが該当します。 (これがいまいちよくわからなければこちらを見てください) 今回の関数だと、導関数は f'(x)=4x(x2+3x+a) ですが、例えば a=0 で f'(x)=4x(x2+3x) の場合だと、f'(x)=4x2(x+3) ということになり、「導関数のグラフ」としてはこの図のようになります。
x=-3 の箇所ではきちんと「負から正に」切り替わっていますので、ここで極小ということになりますが、x=0 の箇所では「正から正」のままになってしまっていて、「極大ではない」という状況になってしまいます。 つまり、極大値と極小値の両方が存在するためには「導関数がx軸と『異なる3点で』交わる」必要があり、今回の場合は x=0 で重解とならないように「x2+3x+a=0 が x=0以外と異なる解を持つ」ケースを考えればいい、というものです。 |
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |