| 〔質問〕 「x個配るとyあまり、a個配るとb個多い…」のような問題の式がたてられません。 また余ったときにプラスにするのか多いときにプラスにするのかがイマイチわからないです。 |
| 〔回答〕 過不足に関する問題は、図に表すと分かり易いです。 言葉だけで考えようとすると間違えやすいので、図を書く習慣をつけましょう。 (例) 子どもたちにアメを3個ずつ配ると40個あまり、5個ずつ配ると6個不足した。 このとき、子どもは何人いますか。 子どもが x人いるとする。 どちらの場合も、「(今ある)アメの数は変わらない」ことを利用して方程式に表します。 ・3個ずつ配ると40個余る → 3x+40(3個ずつ配っても、「さらに」40個ある) ・5個ずつ配ると6個不足 → 5x-6 (5個ずつ配ると、今あるアメの数より「6個オーバー」する) よって、3x+40=5x-6 図に表すと、以下のようになるので、イメージしやすくなります。 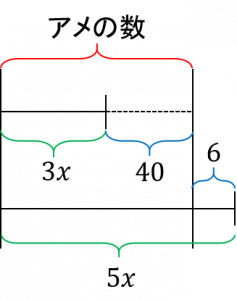 3xと5xの長さを比べると、5xの方が長くなります。(3xの方が短い) このふたつのものを「=の関係」にするには、 「(小さい・短い方)+ 〇 =(大きい・長い方)- ● 」という式の形になります。 今後の考え方の参考にしてみてください。 |
\[\frac{0.03x}{x} \]
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

