| 〔質問〕 l は y=13x+3 のグラフで、m は y=-2x+18 のグラフである。 l上に点A、m上に点D、x軸上に点B、Cをとり四角形ABCDが 正方形になるとき点Aの座標を求めよ。 代入だけではわからなくて困っています。 どう解くのですか |
| 〔回答〕 座標平面上での図形なので、四角形ABCDの頂点の座標を使って考えます。 そのうち、「1点の座標を文字を使って表す」ことで関係式を立てていきます。 四角形ABCDが正方形となるということは、「AB=AD」が成り立つことになりますが、これを数式で表すことを目指します。 点Aのx座標を a とすると、点A (a, 13a+3) となります。 「点Dは点Aとy座標が同じ」「点Bは点Aとx座標が同じ」ことを利用して、2点の座標を a を使って表します。 AB=(点Aのy座標)、AD=(点Dのx座標)-(点Aのx座標) です。 これを使い、AB,ADの長さを表して、「AB=AD」の等式を立てます。 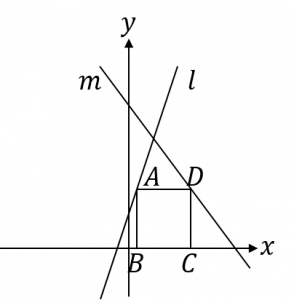 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

