| 〔質問〕 1次関数のグラフをみて、三角形の面積を求める問題の方法を教えてください。 |
| 〔回答〕 具体的な問題ではありませんので、一般的にどう解くのか、という回答をします。 ふつうの図形問題と違って座標平面上で考えることになるので、 「各頂点の座標を使って」底辺の長さや高さを求めながら解いていきます。 もっと詳しくいうと、「x座標同士の差」と「y座標同士の差」を使って考えます。 代表的な2つのパターンを考えます。 (1)x軸上に2点があるタイプ 図のような△ABCの面積を求めます。 三角形の面積は(底辺)×(高さ)×(1/2)で求めることができますので、 (底辺)をBC、(高さ)を点Aから下した垂線の長さと考えます。 すると、△ABC=(点B,Cのx座標の差)×(点Aのy座標)×(1/2)となります。 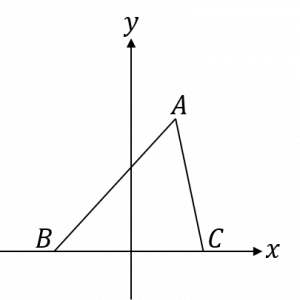 (2)y軸上に頂点があるタイプ 図のような△AOBの面積を求めます。 y軸をまたぐような形の三角形では、「y軸を切り取った長さ」を利用することができます。 A’はAから下した垂線とx軸との交点、B’はBから下した垂線とx軸との交点とすると、 等積変形を利用して、△AOC=△A’OC 、△BOC=△B’OC とすることができます。 すると、△AOB=△AOC+△BOC=△A’OC+△B’OC=△CA’B’ となります。 あとは、(底辺)をA’B’、(高さ)をCOと考えて、 △AOB=(点A’,B’のx座標の差)×(点Cのy座標)×(1/2)と解けばよいです。 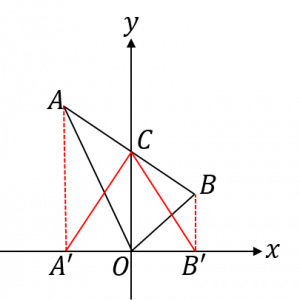 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

