| 〔質問〕 直線上に半径1cmの半円を重ねていきます。次の問いに答えなさい。 (1)重ねる半円が1個増えると、重ねてできる図形の面積はいくら増えますか。 (2)重ねてできる図形の面積が~ |
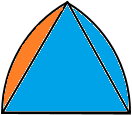
| 〔回答〕 今回の問題のポイントは、「二つの図形が重なり合う部分の面積」を出すことです。 この面積を出すことさえできれば、あとはさほど難しくありません。 重なり合う部分を抜き出すと、下の図のようになります。
(青色で示した部分の面積) (オレンジ色で示した部分の面積) (重なり合う部分の面積) (1) (重ねる半円を1つ増やすと増える面積) (2) よく規則性を使う問題で使う考え方で、 これを使うと、 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |