| 〔質問〕 放物線 y=x2 と傾きが1である直線Lが、2点A、Bで交わり、点AのX座標は-2である。 三角形APBの面積が、18となるようにx軸上に点Pをとった時、点PのX座標を求めなさい。ただし点PのX座標は正とする。 のヒントをくださると光栄です。 |
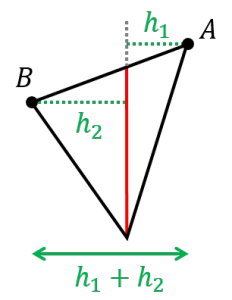
| 〔回答〕 関数のグラフと三角形の面積を合わせた問題を考える際、底辺を図の赤線のように捉えると、右側の三角形の高さが h1、左側の三角形の高さが h2 となります。 全体の面積は、右と左の三角形の合計ですので「底辺×h1×(1/2)+底辺×h2×(1/2)」で求まるわけですが、これは 底辺×(h1+h2)×(1/2) というようにくくることができます。
結果、このような底辺の取り方をすれば、面積は「底辺×(2点のx座標の差)×(1/2)」で求まります。
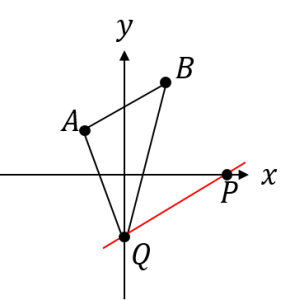
今回の場合、 点Qを通り、ABに平行な直線(傾きがABと同じなので1)の式は この直線とx軸との交点の座標を求めると、点Pの座標が分かります。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |