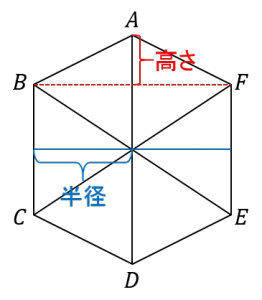
| 〔質問〕 1辺4cmの正六角形がある。この正六角形を、頂点ADを通る直線Lを軸として1回転させてできる立体について次の問いに答えなさい。 (1)表面性を求めなさい。 (2)体積を求めなさい。 (頂点の名前を変更しています) よろしくお願いします。 |
| 〔回答〕 この問題で問われている回転体は、複数の立体を合わせたものです。 上から、円すい・円柱・円すいです。 この問題の場合、半径を求める必要があるため、もとの正六角形から求めます。
さて、今回の回転体の半径を求めていきます。 また、上の部分にできる円すいの高さも求めないといけません。 (1)表面積…(上の円すい)・(真ん中の円柱)・(下の円すい)に分けて考えます (2)体積…(上の円すい)・(真ん中の円柱)・(下の円すい)に分けて考えます |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |