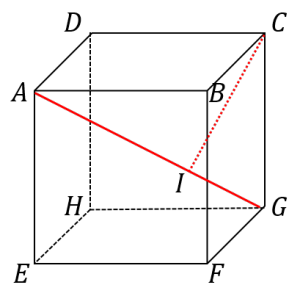
| 〔質問〕 一辺の長さが10cmの立方体ABCD-EFGHがある。次の問いに答えなさい。 (1)線分AGの長さを求めなさい。 (2)頂点Cから線分AGヘ垂線をおろした時、その垂線の長さを求めなさい。 図形が苦手で全然わからないです。 |
| 〔回答〕 直方体や立方体における、奥行きを含む対角線の長さは三平方の定理を使って求めることができます。 各辺の長さを a, b, c とすると、 √(a2+b2+c2) で一度の計算で出ます。 また、垂線の長さを求める問題ですが、「直角三角形内に垂線を下ろすときは面積を使って求める」ことができます。 (1)対角線AGの長さ (2)頂点CからAGに下ろした垂線の長さ(垂線をCIとする)
|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |