【質問】数学（中学）：「角C＝90度の直角三角形ABCの辺AB上に中心Oをとり…」という問題がわかりません

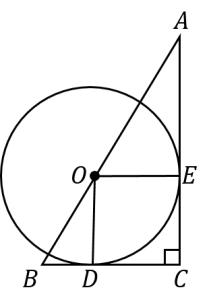
〔質問〕
「角C＝90度の直角三角形ABCの辺AB上に中心Oをとり、2辺AC、BCに接するように円を書いたものである。AC=8cm、BC=4cm の時、円Oの半径を求めよ。」
全然わからないので、よろしくお願いします。

iPhoneアプリは、ないのですか？図を載せたいのですが…

〔回答〕
円を使った問題では、円の性質をきちんと使えるか？ということが問われています。
・円の半径は接線と直角に交わる
・円の半径の長さはその円の中ではどこでも等しい
などです。
分かっていても、問題に活かせないことが多いので注意しましょう。

今回の問題を図に表すと、以下のようになります。

11638

円Oは「中心がAB上にあり、ACとBCに接する」円ですので、OE＝OC（半径）となります。
また、AC, BCは円Oの接線となるので、∠OEA＝∠ODB＝90°となります。（半径と接線は直角に交わる）
よって、「四角形ODCEは正方形である」とわかり、
OE＝EC（＝OD＝DC）…①　といえます。

また、
△ABCと△AOEにおいて、
∠BAC＝∠OAE（共通）、∠ACB＝∠AEO＝90°より、
二組の角がそれぞれ等しいので、△ABC∽△AOE…②　です。

相似な図形の対応する辺の比は等しいので、
②より　AC：BC＝AE：OE＝8：4＝2：1
AE：OE＝AE：EC＝2：1（①より）

AC＝8なので、
EC＝8×（1/3）＝8/3
EC＝OEですので、こちらが半径となります。

iPhoneアプリについては現在開発中で、春頃のリリースを予定しています。それまでの間は申し訳ありませんが、現在の形でお願いいたします

アンケートへのご協力をお願いします（所要２～３分）
「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします（Googleフォームにアクセスします）