| 〔質問〕 xyz空間において、 方程式 x2+y2+z2=6x-2z …(1) の表す曲面と、 平面α:2x-2y+z=-1 …(2) との交わりは何か、という問題で、 (1)と(2)を連立させると、 5x2-8xy+5y2-6x-1=0 と出るのですが、これは円の方程式ではありません。 しかし、実際は中心が(5/3, 4/3, -5/3)で半径が√6の円となります。なぜ私のやり方ではきちんと円の方程式が出なかったのでしょうか? |
| 〔回答〕 ものすごくいい質問だと思います。 簡単に解説すると、この連立方程式を解く際に「zを消す」という作業をしていますが、これは断面に関しての「x, y の関係のみを表す式」となってしまっています。 つまり、球や断面などを「上から眺めた」様子を表しているのです ※ 以下の図の座標や形などは適当です。イメージとして使ってください 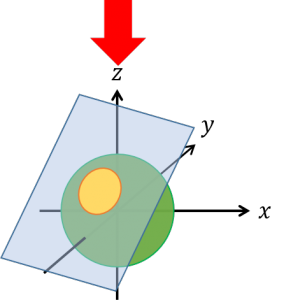 〔上から見た図〕  この時、切断した平面に対しては「斜め」に見ていることになりますので、結果、断面も歪んでしまいます。 ※ 実際に求まった式は「楕円」の方程式になっています ※ 連立方程式の計算としては、5x2-8xy+5y2-6x-1=0 を満たす(x, y)で、そのときの z座標が z=-2x+2y-1 となる、とすれば誤りではありません。ただ、これを見ただけでは円の気配が全くしませんが… 一方で、正しいのは「断面に対して真っ直ぐに見る」ことで、そのときに「円」が現れます。 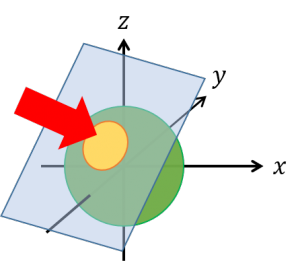 実際の解き方としては、 (1)球の中心から、平面 2x-2y+z=-1 に垂線をおろす。その足(Hとおく)が、求める断面の円の中心 平面の方程式が 2x-2y+z=-1 なので法線ベクトルの成分が(2, -2, 1)とわかる。 これを用いて(球の中心を通る)空間の直線の式を立てて、平面の式と連立させる。 (2)円の半径は三平方の定理を用いて求める 球の中心(Pとする)、垂線の足(H)、断面の円上の任意の点をQ とすると、△PHQ は ∠H が 90° の直角三角形。 PHは垂線の足の長さ(点と直線の距離の公式から求まる)、PQ は球の半径なので、ここから HQ の長さが求まる。 ※ 断面が円となるのは所与のものとして扱っていいと思います。また、実際に円の方程式を求めようとしても(中心からの距離=半径)、空間内で考えれば結局「球」の方程式になってしまいます。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

