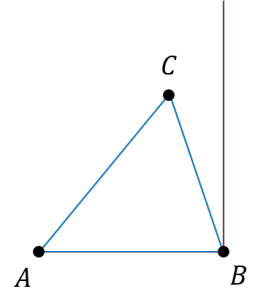
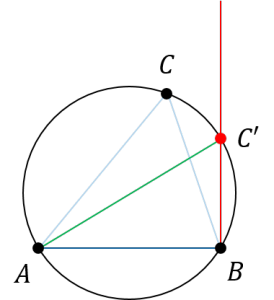
| 〔質問〕 同一直線上にない3点が平面上に指定された場合、必ずそれらの点を通る円が描けることを証明してください。 (三角形に外接円が必ず存在する理由) |
| 〔回答〕 例えば、以下の感じでどうでしょうか? 「同一直線上にない3点」ということですから、これを「△ABC」とします。 まず、これが直角三角形であるときは、そのまま外接円が存在すると言うことができます。 厳密な説明としては、例えば∠Bが直角のとき、辺ABと辺BCの垂直二等分線を引けば、それぞれ中点連結定理から、辺ACとはその中点(M)でぶつかることになります。 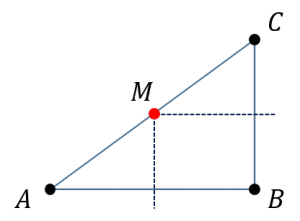 そして、「垂直二等分線」ということは、AMとBMは長さが等しく(△ABMが二等辺三角形になるため)、またBMとCMも長さが等しくなります(△BCMが二等辺三角形)。よって、点Mから点A,B,Cまでの距離がそれぞれ等しいので、ここを中心とする円を描けます。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |