【解説】
まず、文章題では「問われている未知数を x,y を使って表す」のが基本なので、
A町からB町の距離を x km、B町からC町の距離を y kmとします。

ここで問題をよく読むと、

・A町からB町を経てC町までの道のり（距離）は26km…①
・全体では6時間かかった（進んだ合計時間が6時間）…②

であることが分かります。

また、図に示すと、

これを使って式を立てると、

・A町からB町を経てC町までの道のり（距離）は26km
⇒ [A町からB町の距離]＋[B町からC町の距離]＝26km
⇒ x＋y＝26 …①

・全体では6時間かかった（進んだ合計時間が6時間）
⇒[A町～B町にかかる時間]＋[B町～C町にかかる時間]＝6時間
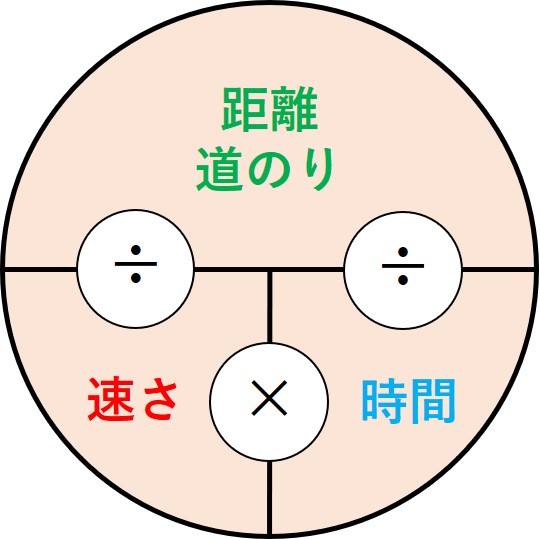
（[時間]＝[道のり] / [速さ] より）
⇒ (x/3)＋(y/5)＝6…②
 
 
x＋y＝26 …①
(x/3)＋(y/5)＝6…②
このように、①, ②の式を立てることができたので、連立方程式を解くと、
x＝6, y＝20

つまり、
「A町からB町の距離が6km、B町からC町の距離が20km」ということになり、
これらは「問題に適している」。
（今回の x,y は距離なので、正の数である）

〔答え〕A町からB町の距離が6km、B町からC町の距離が20km

＜補足＞

「速さに関する文章題」では、
・進んだ距離の合計についての式
・かかった時間の合計についての式
を立てて、解き進めることが多いです。

式を立てるには、「道のり・速さ・時間」の関係をしっかり頭に入れておくことが大切です。

＜まとめ＞

・文章題では「問われている未知数を x,y を使って表す」のが基本
・速さに関する問題では「道のり・速さ・時間」の関係を使う
・求めた解が「問題に適しているか」を確認する