<ポイント>
・どちらにも進行しない(ように見える)波を定常波という
・反対向きに同じ速さで進む「波長・振幅が等しい」波が重なるときに、定常波ができる
・定常波の「全く振動しないところ」を節、「大きく振動するところ」を腹という
・どちらにも進行しない(ように見える)波を定常波という
・反対向きに同じ速さで進む「波長・振幅が等しい」波が重なるときに、定常波ができる
・定常波の「全く振動しないところ」を節、「大きく振動するところ」を腹という
(1)定常波
反対向きに同じ速さで進む「波長と振幅が等しい正弦波」が重なると、合成波はどちらにも進んでいないように見える。
このような波形が「進行しない波」を定常波といいます。
(これに対して、「波形が進行する波」を進行波といいます)
反対向きに同じ速さで進む「波長と振幅が等しい正弦波」が重なると、合成波はどちらにも進んでいないように見える。
このような波形が「進行しない波」を定常波といいます。
(これに対して、「波形が進行する波」を進行波といいます)
(2)定常波のグラフ
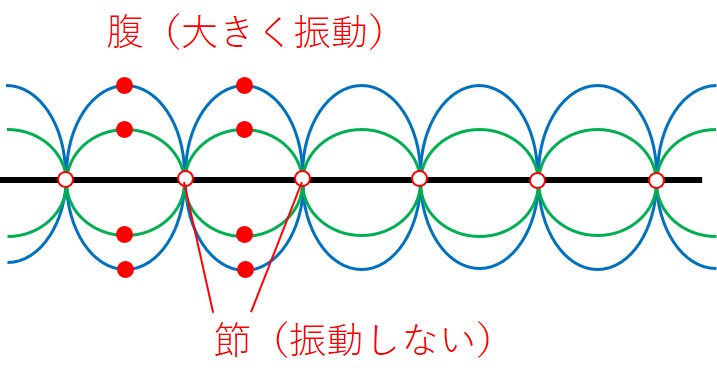
定常波の波形のグラフを見ると、「大きく振動している」点と、「まったく振動していない点」が交互に並んでいるのがわかります。
「大きく振動している」点を腹(はら)といい、「まったく振動していない点」を節(ふし)といいます。
なお、「腹から腹」「節から節」までの距離は、ともに半波長分になるため λ/2 となります。
また腹の部分で見られる最大の振幅は 2A となります。
(それぞれの波の振幅の和)
なお、「周期は進行してくるそれぞれのものと同じ」になります。
<補足>
2つの波源から同じ位相で進んでくるとき、その「中点を原点として、腹・節の位置」を求めることができます。
2つの波源から同じ位相で進んでくるとき、その「中点を原点として、腹・節の位置」を求めることができます。
腹: x = ± m・(λ/2) (m=0, 1, 2, …)
節: x = ± (2m+1)・(λ/4) (m=0, 1, 2, …)
<まとめ>
・どちらにも進行しない(ように見える)波を定常波という
・反対向きに同じ速さで進む「波長・振幅が等しい」波が重なるときに、定常波ができる
・定常波の「全く振動しないところ」を節、「大きく振動するところ」を腹という
・どちらにも進行しない(ように見える)波を定常波という
・反対向きに同じ速さで進む「波長・振幅が等しい」波が重なるときに、定常波ができる
・定常波の「全く振動しないところ」を節、「大きく振動するところ」を腹という
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|


