（１）波長
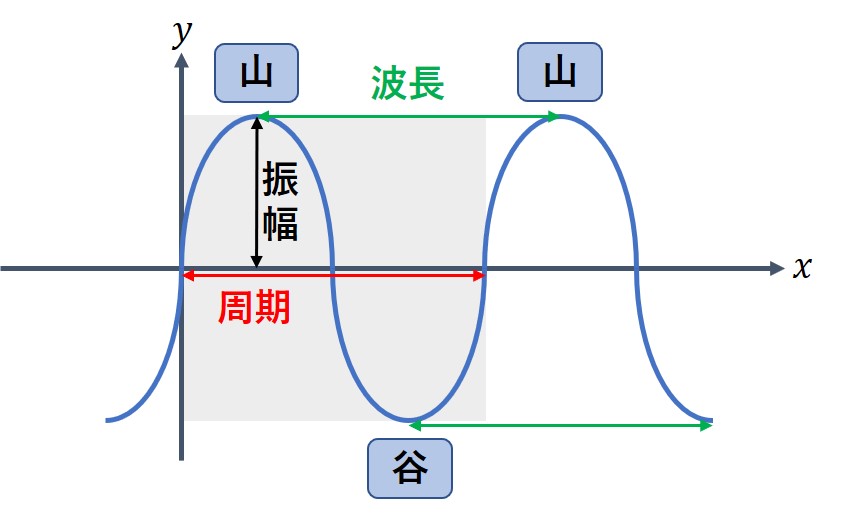
波において、「同じ状態にある」隣りあう2点間の距離を波長といいます。
言い方を変えれば、「ある点から、同じ状態に戻るまでの長さ」ともいえます。
つまり、「波一つ分の長さ」を波長といいます。

上図において、山と山・谷と谷の間の距離を波長としていますが、（となり合う）「同じ変位 y の点」どうしの距離はどこでも等しくなっていて、波長として考えることができます。

ふつう、波長は「 λ（ラムダ）」を使って表します。

（２）振幅
「振動の中心と最大の変位までの幅」を振幅といいます。
「振動の中心から山まで」「振動の中心から谷まで」の幅のことです。

なお、「山と谷」の幅のことを波高といいます。

（３）周期
媒質中の１点における振動が、１回終了するごとに「波形は１波長λの分だけ前進」します。
このときにかかる時間を周期といいます。
（「山（谷）がきてから、次の山（谷）がくるまでの時間」とイメージすると分かりやすい）

ふつう、周期は「T」を使って表します。

（４）振動数
「単位時間（ふつう１秒間）に媒質の１点を通過する波の数」を振動数（または周波数）といいます。
これは「媒質の１秒間の振動回数」と考えることもできます。

振動数（周波数）の単位は「Hz（ヘルツ）」を使います。
（１秒間に１回振動すると、１Hz）

ふつう、振動数は「f」を使って表します。

＜補足＞
波形において、「媒質の変位が最大になっている」部分を山、「媒質の変位が負の方向に最大になっている」部分を谷といいます。
波形を見た目通りにとらえてもらって、「上にふくらんでいる部分」が山、「下にへこんでいる部分」が谷だと考えましょう。

＜まとめ＞
・波において、「同じ状態にある」となり合う2点間の距離を波長という
・「振動の中心と最大の変位までの幅」を振幅という
・媒質の「1秒間に振動する回数」を振動数という