（１）仕事
「物体に力を加えて、力を加えた方向に動かすこと」を仕事といいます。
これを「力は物体に対して仕事をした」といいます。

（２）力を加えた方向に物体が移動する場合の仕事
仕事 W [ J ]＝力の大きさ F [ N ]・移動距離 s [ m ]

たとえば、物体を 10 N の力で引いて、引いた方向に 2 m 動いたとします。
このとき、引いた手が物体にした仕事 W は、 10×2 ＝ 20 [ J ] となります。

（３）力の向きと移動する向きが異なる場合

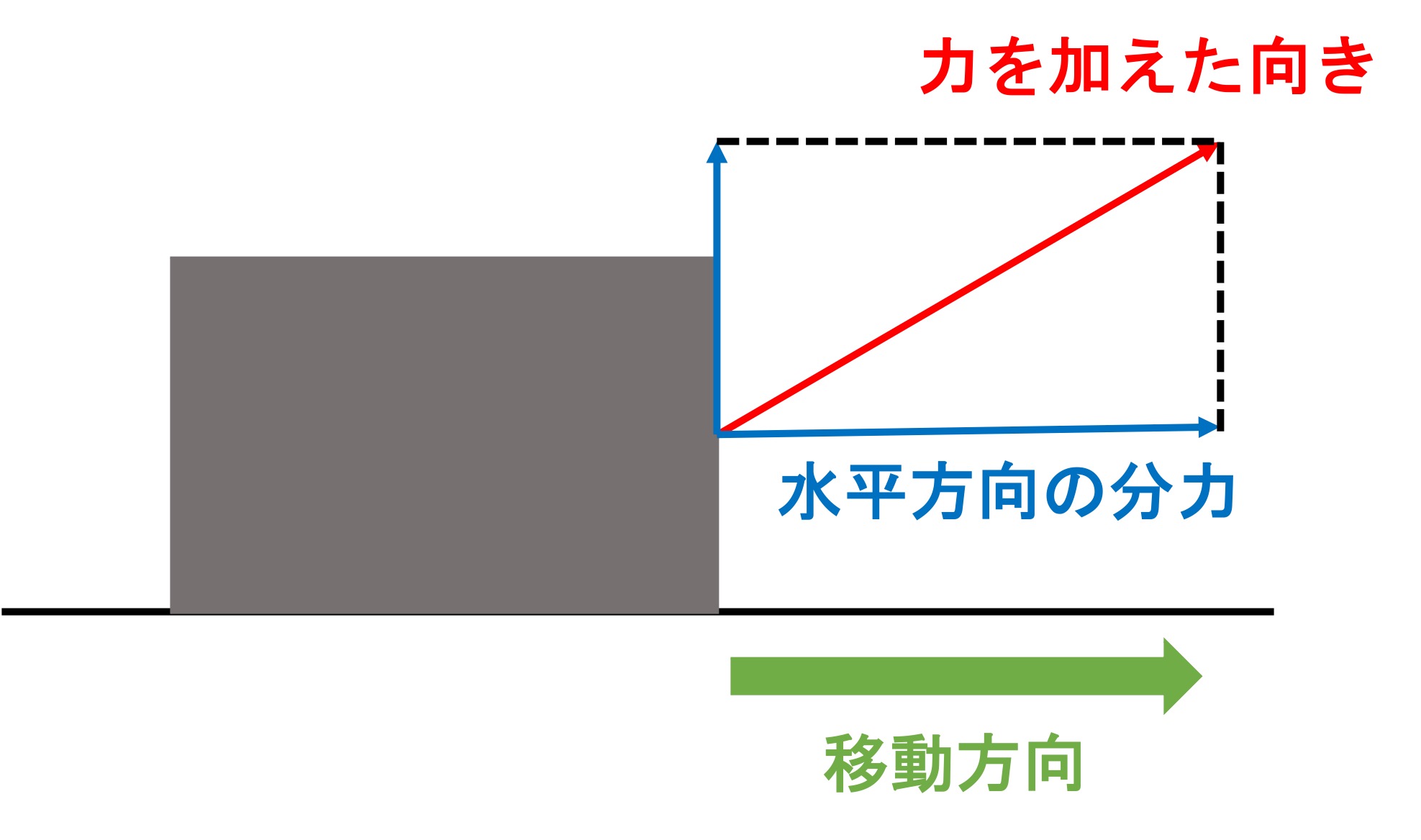
この場合は、力を分解して「水平方向の分力」を用いて計算します。
「力を加えた向き」と「水平方向」とのなす角をθとすると、
〔水平方向の分力〕＝加えた力 F ・cosθ　となります。

よって、
仕事W[J]＝力F[N]・移動距離s[m]・cosθ

なお、この θ の値によって、仕事 W の符号が変わります。
0≦θ＜90°の場合、W＞0
θ＝90°の場合、W＝0
90°＜θ≦180°の場合、W＜0

＜補足＞
・物体に力を加えたが、物体が動かなかった場合
　仕事＝0J となります。
　①の動かした距離＝0 なので、積は0となってしまいます。

・物体を持ち上げて動かない場合
　仕事＝0J となります。
　①の動かした距離＝0 なので、積は0となってしまいます。

・物体を持ち上げて、そのまま支えて水平方向に移動した場合
　仕事＝0J となります。
「物体に力を加えて、力を加えた方向に動かすこと」を仕事というので、移動方向への分力が0Nとなります。つまり、「力を加える方向」と「移動する方向」が垂直な場合は、いくら力を加えても仕事は 0 のままです。

＜まとめ＞
・「物体に力を加えて、力を加えた方向に動かすこと」を仕事という
・力を加えた方向と移動する方向が同じなら　仕事W[J]＝力F[N]・移動距離s[m]
・力を加えた方向と移動する方向が違うなら　仕事W[J]＝力F[N]・移動距離s[m]・cosθ