<ポイント>
・「物体がどの向きにどれだけ移動したか」を表す量を変位という(位置の変化)
・変位はベクトル量である
・「基準点から注目する点まで引いたベクトル」を位置ベクトルという
・「物体がどの向きにどれだけ移動したか」を表す量を変位という(位置の変化)
・変位はベクトル量である
・「基準点から注目する点まで引いたベクトル」を位置ベクトルという
(1)変位
運動している物体について、「物体がどの向きにどれだけ移動したか」を表す量を変位といいます。
「移動する前の位置」と「移動した後の位置」を比べたとき、その「位置の変化」が変位ということです。
運動している物体について、「物体がどの向きにどれだけ移動したか」を表す量を変位といいます。
「移動する前の位置」と「移動した後の位置」を比べたとき、その「位置の変化」が変位ということです。
変位は「位置の変化」なので、単純に「どれだけ移動したのか」という大きさだけでなく、「どの向きに移動したのか」を考える必要があります。
つまり、「大きさと向きをもつ」ということになるので、変位はベクトル量です。
(2)位置ベクトル
「基準点から注目する点まで引いたベクトル」を位置ベクトルといいます。
基準となる点から、物体がある位置までを結んだもので、「大きさと向き」を持ちます。
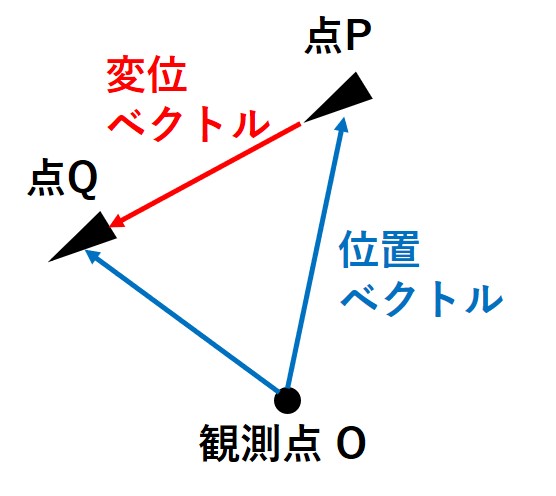
(以下の説明において、[ ]はベクトルを表すとします)
こちらの図でいえば、移動する前の[OP], 移動した後の[OQ]がそれぞれの位置ベクトルとなっています。
また、移動のようすを表した[PQ]は「変位ベクトル」となります。
補足
数学Bのベクトルの単元で習う内容になりますが、
変位ベクトル[PQ]は、「位置ベクトルの差」で求めることができます。
〔変位ベクトル〕=〔移動後の位置ベクトル〕-〔移動前の位置ベクトル〕
となるので、
[PQ]=[OQ]-[OP]
と考えることができます。
<まとめ>
・「物体がどの向きにどれだけ移動したか」を表す量を変位という(位置の変化)
・変位はベクトル量である
・「基準点から注目する点まで引いたベクトル」を位置ベクトルという
・「物体がどの向きにどれだけ移動したか」を表す量を変位という(位置の変化)
・変位はベクトル量である
・「基準点から注目する点まで引いたベクトル」を位置ベクトルという
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|


