電気回路自体を水路にたとえたとき、
回路の中にある抵抗にかかる電圧は「水の落差」だとイメージすると分かりやすいです。

回路を流れる電流を水だとイメージしたとき、「水は高いところから低いところへ流れていく」ことになります。
電池などの「電源が水を高いところへくみ上げるはたらき」をしていて、その高さから「抵抗のある部分で下に流れる」というイメージです。
そして、電源まで流れて戻った水（＝電気）は高いところまで引き上げられる、というサイクルです。

この電圧の大きさを表すとき、単位は V（ボルト）を使います。

（１）直列回路の電圧
直列回路の各部分にかかる電圧の和は、全体に加わる電圧（電源の電圧）に等しい。

この回路の場合は、電源電圧V＝V_A＋V_B という関係が成り立ちます。
これは抵抗が３つ以上になっても同じで、電源の電圧は各部にかかる電圧の和に等しくなります。

「電源で高いところに引き上げられた水が、２回下に落ちてから電源に戻った」と考えれば、
「落ちた高さの合計＝引き上げられた高さ」となるからです。

（２）並列回路の電圧
並列に接続された抵抗にかかる電圧は等しくなります。

この回路の場合は、電源電圧V＝V_A＝V_B という関係が成り立ちます。

それぞれの抵抗でかかる電圧の大きさが同じにならないと、「水の落差が異なる」ということになって、高さの違う水は合流できません。そのため、「同じ高さだけ落ちているはず」と考えます。

＜補足＞

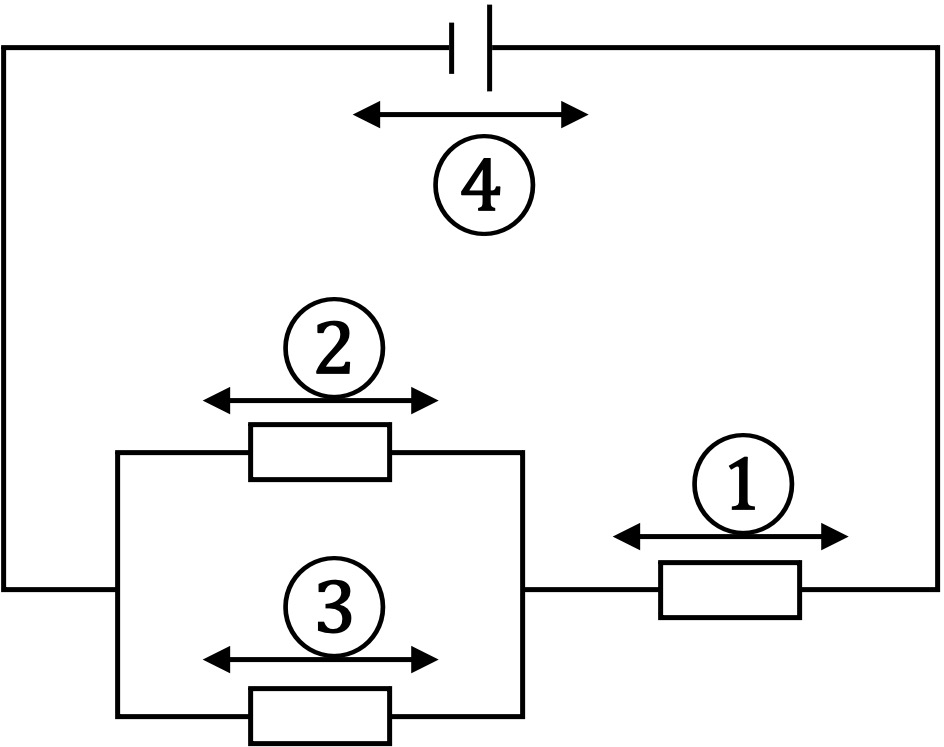
このような、直列回路と並列回路の組み合わせのものも考えてみます。
①〜④をそれぞれの部分にかかる電圧だとすると、

②＝③が成り立つ（並列につながれた部分の電圧は等しい）ので、
④＝①＋②＝①＋③（直列につながれた抵抗にかかる電圧の和は、電源の電圧に等しい）
となります。

＜まとめ＞
・（抵抗にかかる）電圧は「水の落差」とイメージする
・直列回路：電源電圧V＝V_A＋V_B
・並列回路：電源電圧V＝V_A＝V_B