〔問題〕
x軸上を運動する物体の運動について考えます。時刻 t＝0s に初速度 0m/s で出発し、以下のように加速度を変化させながら運動したとする。

・ 0≦t＜5.0　加速度 0.80m/s²の等加速度直線運動
・ 5.0≦t＜15.0　等速直線運動
・ 15.0≦t≦25.0　加速度 －0.40m/s²の等加速度直線運動

（１） 5.0≦t＜15.0 の等速直線運動をしているときの、物体の速度 v₂ を求めなさい。
（２）t＝5.0s, 15.0s, 25.0s のときの物体の位置 x₁, x₂, x₃ をそれぞれ求めなさい。

〔解説〕
まずは、各区間において、どのような運動をしているのかを確認します。
・ 0≦t＜5.0　加速度 0.80m/s²の等加速度直線運動
　→速度 0 の状態から加速していく（加速度が正のため）

・ 5.0≦t＜15.0　等速直線運動
　→ 0≦t＜5.0　で加速したあとの速度を維持している

・ 15.0≦t≦25.0　加速度 －0.40m/s²の等加速度直線運動
　→速度がある状態から減速していく（加速度が負のため）

（１） 5.0≦t＜15.0 の等速直線運動をしているときの、物体の速度 v₂ を求めなさい。

はじめの 0≦t＜5.0 の間に加速した速度のまま、 5.0≦t＜15.0 の間に等速直線運動をします。
したがって、t ＝ 5.0s のときの速度を求めればOKです。

v ＝ v₀ ＋ at より、
v₂ ＝ 0 ＋ 0.80・5.0 ＝ 4.0m/s

（２）（２）t＝5.0s, 15.0s, 25.0s のときの物体の位置 x₁, x₂, x₃ をそれぞれ求めなさい。

等速直線運動と等加速度直線運動が続く問題では、「v-tグラフ」を描くと分かりやすいです。
（特に問題で指示がなくても、「描いてみる」という習慣をつけましょう）

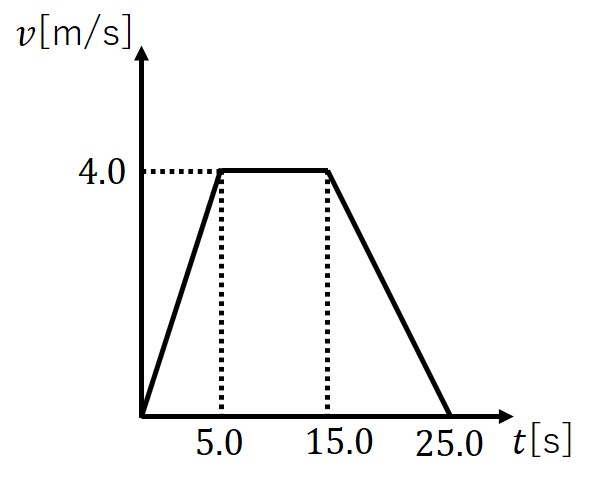
「v-tグラフ」で、「x軸とグラフで囲まれた部分の面積は移動距離となる」ことを利用します。

x₁ ＝ (1/2)・5.0・4.0 ＝ 10.0[m]
x₂ ＝ x₁ ＋ 4.0・10.0 ＝ 50.0[m]
x₃ ＝ x₂ ＋ (1/2)・10.0・4.0 ＝ 70.0[m]

このように、「v-tグラフ」を使うことで、「移動距離を三角形・長方形の面積で求める」と計算がずいぶん楽になります。
積極的に使っていきましょう！

＜まとめ＞
・問題文より、各時刻における運動のようすを読み取る
・〔等加速度直線運動〕瞬間の速さ v ＝ v₀ ＋ at
・「v-tグラフ」で、「x軸とグラフで囲まれた部分の面積は移動距離となる」