〔回答〕
まず、全体的にですが、「問題文における必要条件・十分条件」については、あくまでも「強いて言えば」くらいのことですので、あまり気にし過ぎない方がいいかなと思いますよ。
もちろん、はっきりと「p⇒q」とか「pならばq」の問題であれば意識しないといけませんが、
・原則として、話は必要十分条件(完全なる言い換え)で進めていく
・「●●のとき」は「あくまでもその範囲内だけで考える」というだけの話
です。
(後者のことを、強いて言えなら、「●●のとき」というのが「(答えから見れば)必要条件」に該当する、というもの) (補足)
「●●のとき××を求めよ」の場合、「●●かつ××」を求めるわけですが、
この「●●かつ××」が実際には文章だったりもしてまだまだよくわからないので、
「●●かつ××」を同値変形で言い換えていって、最終的に「●●かつ×× というのは a=3 のときだ」(●●かつ×× ⇔ a=3)みたいにする、というのが基本的な進め方です。 |
それを踏まえて、質問に関してですが、 (1)●●のときは「必要条件」なのですね。P→QではPが十分条件となっていますがこのあたりはどう理解しておけばいいでしょうか? p⇒q が真のとき、包含関係としては「条件pを満たすものの集合 ⊂ 条件qを満たすものの集合」という関係になっていて、
その点で、「実際の答え ⊂ ●●」と同じ関係性になっていることになります。
(2)「a>0 のとき、a2-1>0 の解は?」の例ではa>0は必要条件ですがa2-1>0の部分は何条件になるのでしょうか?「解は」まで含めて十分条件ですか? 前述の通り、あまり意識しすぎない方がいいと思いますが、あくまでも強いて言えば「(a>0 かつ) a2-1>0」というのが十分条件に相当します。
※ 正確には「a>0 かつ」を入れる必要がありました。前回の質問文の方の回答文も一部修正しています。 正確には下記のような関係性で、要は「赤の部分(答え)が、a>0 に対する部分集合になっている」ということが理解できればいいです。
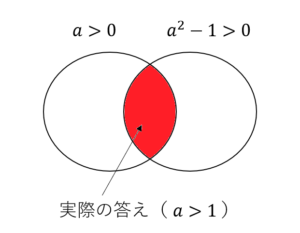
(3)参照HP1にある(1)「~のとき」「~ならば」は必要条件を表しているのであれば(2)「𝑝となるような𝑞」と記載がある場合は何条件になるのでしょうか?(そもそも「~のとき」「~ならば」なら必要条件のみで、「𝑝となるような𝑞」となっていれば必要十分条件を示す必要があるというのは日本語的にどう違うのでしょうか?) 例えば、2次関数 y=x2+2x+c について「『x軸と共有点を持つ』となるような『cの範囲』」というケースで考えてみると、
実際に計算してもらったら、『x軸と共有点を持つ』の完全なる言い換えが『c≦1』ということになり、
別の言い方をすれば、『x軸と共有点を持つ』グラフを全部列挙した場合と、『c≦1』のグラフを全部列挙した場合とでは全く同じ要素が列挙されることになります。
この「完全なる言い換え」としての『c≦1』を求めて欲しいというのが、参照HPでいう「必要十分条件」です。 ※ 結局、集合としては同じものを考えますので、どっちを必要条件・十分条件と見ても支障ないことにはなります。ただし、ふつう『x軸と共有点を持つ』という話に対して数例だけを答える(『少なくとも c=0 は該当する』とだけ答える)みたいなことはないでしょうから、(「答え」に対してこちら側が、少なくとも大きい方の集合にはならないという意味で)十分条件側だ、と想定しても構いません
一方、もし「c>0 のとき」という条件があれば、あくまでもこの範囲の中でのものとして『0<c≦1』というのが答えになるわけですが、
となると、『0<c≦1』は『c>0』の部分集合ですから、強いて言えば「c>0」は答え(0<c≦1)に対する必要条件ということになるなあ、という話です。
(4)問題文が複雑なときは文のどの部分が必要条件でどの部分が十分条件であるかなどはどのように判断していけばいいでしょうか?範囲が広いものを必要条件とみなしていけばいいのでしょうか? 冒頭の通り、むしろ変に意識しない方がいいです。
「●●のとき」という条件をかけられていたときに、「あくまでもその範囲で考える」とだけ思うくらいで大丈夫で(「答え」から見れば「この条件」の部分集合であるため、強いて言うなら(「この条件」の方が)必要条件というだけの話)、
進め方はあくまでも上記(補足)欄のようなことです。
(5)参照HP2の動画の冒頭にあるような「必要性」での数式の変形とは必要条件の数式を変形していくという理解でいいのでしょうか?
(6)数式の変形には同値変形とそうでない変形があると思われますが自分が今おこなっている操作が同値変形で⇔をつけるべきかそうでないかわかないのですがこの点はどう考えればいいでしょうか?(例えば参照HP2の5分ころの板書の解答1と2の違いがわかりません) ふつう、式変形というのは(無意識ながら)同値での処理はできています。
ですので、もし書くのであれば毎回「⇔」をつければいいくらいの話です。
(それもめんどくさいので、逆に、毎回書いていない) (5)に関しては、「式変形において同値性が崩れる」というのが言いたいものです。
高校数学の範囲で同値性が崩れる場合というのは、実際のところは、
・両辺の2乗
・連立方程式で2式を加減する場合
くらいのもので、この2件が生じたときに注意を払えばそれで事足ります。 ターンナップでも下記の動画を用意していますので、ぜひ見てみてください
・必要条件の意味合い
・同値性が崩れるケース(次の段階で「必要条件に話が広がってしまう」ケース) | 

