「位置エネルギーと運動エネルギーの和」を力学的エネルギーといいます。
〔力学的エネルギー E 〕＝〔運動エネルギー K 〕＋〔位置エネルギー U 〕

「高い位置から球を転がして、そのまま坂を上らせる」という運動を考えます。

高い位置に静止した状態で球があるとき、位置エネルギーをたくさん持っています。
ただし、静止しているのであれば、運動エネルギーはありません。

ここから、球を転がし始めると、だんだん（最下点に向かって）加速していきます。
このとき、「位置エネルギーは減っていくが、運動エネルギーは大きくなって」いきます。
坂を上るときには、この逆のことが起こります。

つまり、位置エネルギーと運動エネルギーは「片方が減少すると、その分他方が増加する」という関係にあるのです。

このとき、摩擦や空気抵抗などの外部からの力がはたらかなければ、「力学的エネルギーの大きさは変わらない」のです。
このことを、力学的エネルギー保存の法則といいます。

「力学的エネルギー保存の法則」は、「球を斜面を使って転がす」場合だけでなく、糸でつるしたふりこの運動でも成り立ちます。

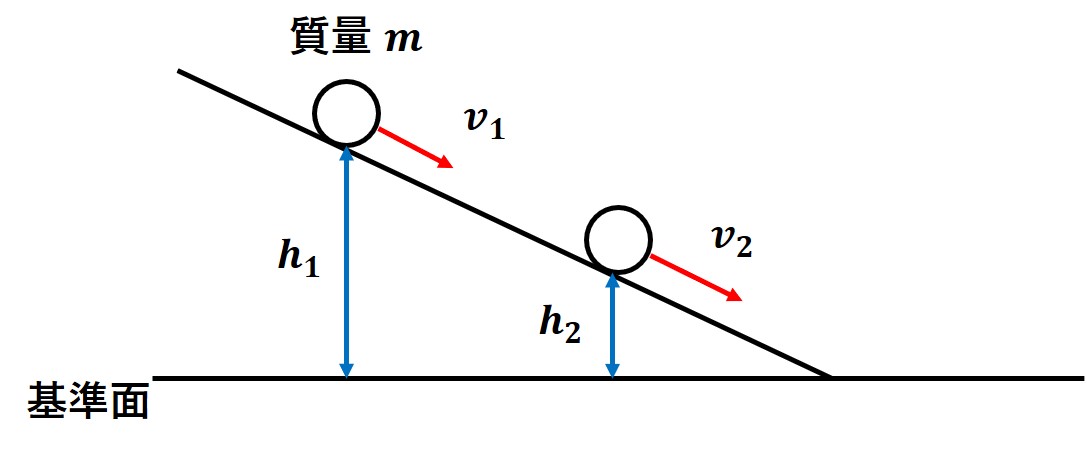
このように、質量mの物体がなめらかな斜面をくだっているとき、
(1/2)mv₁²＋mgh₁＝(1/2)mv₂²＋mgh₂
というように、力学的エネルギー保存則が成り立ちます。

＜補足＞

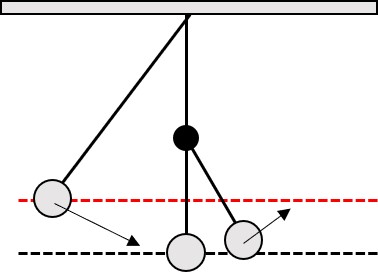
図のように、ふりこの長さを途中で変えたとしても、ふりこが上がる高さは「はじめと同じ高さ」となります。
（力学エネルギー保存の法則より、速さが 0 になるのは、もとの高さまで上ったときとなるため）

＜まとめ＞
・「位置エネルギーと運動エネルギーの和」を力学的エネルギーという
・摩擦や空気抵抗などの外部からの力がはたらかなければ、力学的エネルギーの大きさは変わらない
・「力学的エネルギーの大きさは変わらない」という法則を力学的エネルギー保存の法則という