（１）加速度
単位時間あたりの「速度変化の割合」を加速度といいます。
（物理基礎範囲において）ふつう、1秒あたりの速度変化を考えます。

加速度の求め方は、
〔加速度 a 〕＝〔速度の変化〕/〔時刻の変化〕となります。
もう少し詳しくみると、
〔加速度 a 〕＝〔変化後の速度 v₂－変化前の速度 v₁〕/〔〔変化後の時刻 t₂－変化前の時刻 t₁〕〕となります。

加速度 a が正であるとき、その運動は加速していることになり、
加速度 a が負であるとき、その運動は減速していることになります。

たとえば、一定の割合で加速・減速を行うとき、
車が発進してから30秒で15m/sとなり、そこからブレーキをかけて15秒後に停止したとします。
〔加速時の加速度〕＝(15－0) / 30＝0.5m/s²
〔減速時の加速度〕＝(0－15) / 15＝－1.0m/s²
となり、「加速していると正の値」を、「減速していると負の値」をとります。

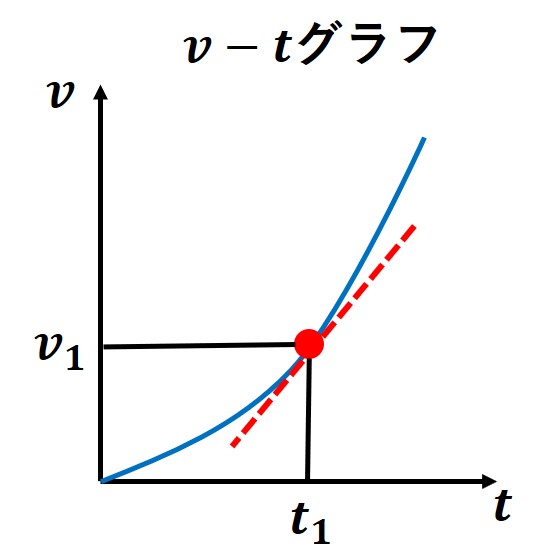
（２）「v – t グラフ」と加速度の関係
「v – t グラフ」における、そのグラフの接線の傾きは（その瞬間の）加速度の大きさを表します。
等速直線運動の場合、「v – t グラフ」は t 軸に平行となるため、加速度が 0 です。
等加速度直線運動の場合、直線で表されるので、その直線の傾きそのものが加速度を表しています。

＜補足＞
〔速度の変化〕や〔時刻の変化〕を表すとき、「Δ（デルタ）」が使われることがあります。
「Δ（デルタ）」は変化量を表す記号なので、Δv であれば速度の変化を、Δt であれば時刻の変化を表しています。

＜まとめ＞
・単位時間あたりの「速度変化の割合」を加速度という
・加速度は速度変化から求めるものなので、ベクトル量である
・加速度は「v – t グラフ」の接線の傾きの大きさとなっている